Колебания

2. На горизонтальной плоскости лежат два шарика массами m₁ и m₂, скрепленные между собой пружинкой жесткостью k. Плоскость гладкая. Шарики сдвигают, сжимая пружину, затем их одновременно отпускают. Определите период возникших колебаний шариков.

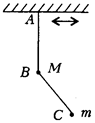
119. К маятнику АВ с шариком массой М подвешен маятник ВС с шариком массой m. Точка А совершает колебания в горизонтальном направлении с периодом Т. Найдите длину нити ВС, если известно, что нить АВ все время остается вертикальной.

129. Тело находится в точке А внутри неподвижной полой сферы. В каком случае тело скорее достигнет нижней точки В сферы: если оно будет скользить по поверхности сферы или если будет скользить вдоль прямой АВ? Трение в обоих случаях пренебрежимо мало, начальная скорость тела равна нулю, а расстояние АВ много меньше радиуса сферы.

177. Частота колебаний струны зависит от ее длины, натяжения и от погонной плотности — массы единицы длины струны. Определите вид этих зависимостей.

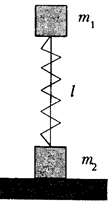
195. Между двумя кубиками массами m₁ и m₂ находится сжатая пружина жесткостью k. Кубики связаны ниткой, расстояние между ними l. На какую высоту поднимется центр масс системы, если нить пережечь? Пружину считать невесомой. Ее длина в нормальном состоянии равна l₀.

230. На систему, состоящую из двух соединенных пружиной шариков массой m и покоящуюся на гладкой горизонтальной поверхности, налетает слева шарик массой М. Происходит лобовой абсолютно упругий удар. Найдите приближенно отношение масс m/М, при котором удар произойдет еще раз.

240. Шар-зонд, имеющий нерастяжимую оболочку, поднялся на максимальную высоту и совершает малые колебания около равновесного уровня. Найдите период этих колебаний, считая, что на такой высоте плотность воздуха r убывает с высотой равномерно на 1,2% через каждые h = 100 м. Трением шара о воздух пренебречь.

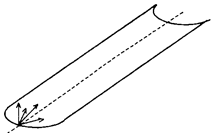
292. Из одной точки на дне горизонтального кругового желоба разлетаются шарики под небольшими углами к образующей желоба с одинаковыми проекциями скорости вдоль этой образующей. Встретятся ли эти шарики?

321. На горизонтальную мембрану насыпан мелкий песок. Мембрана совершает колебания с частотой n = 500 Гц в вертикальной плоскости. Какова амплитуда колебаний мембраны, если песчинки подскакивают на высоту h = 3 мм по отношению к положению равновесия мембраны?

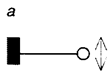
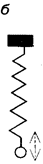
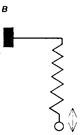
325. Частота малых гармонических колебаний тяжелого шара на легкой закрепленной в стене спице (рис. а) равна n₁, а частота колебаний этого шара на прикрепленной к потолку пружине (рис. б) равна n₂. Какой будет частота колебаний шара на той же пружине, прикрепленной к спице (рис. в)?

346. Одна из обкладок плоского конденсатора площадью S подвешена на пружине. Другая обкладка закреплена неподвижно. Расстояние между пластинами в начальный момент равно l₀. Конденсатор на короткое время подключили к батарее, и он зарядился до напряжения U. Какой должна быть жесткость пружины, чтобы не происходило касания пластин? Смещением пластины за время заряда можно пренебречь.

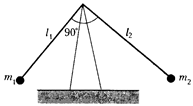
380. Найдите период малых колебаний системы, изображенной на рисунке. Стержни считать невесомыми, их длины l₁ и l₂, массы шаров m₁ и m₂.

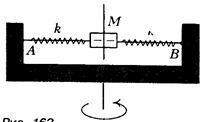
435. В установке, показанной на рисунке, муфта М прикреплена к двум одинаковым пружинам, жесткости которых k = 10 Н/м. Муфта без трения может скользить по горизонтальному стержню АВ. Установка вращается с постоянной угловой скоростью w = 4,4 рад/с вокруг вертикальной оси, проходящей через середину стержня. Найдите период малых колебаний муфты. Масса муфты М = 0,2 кг. При каком значении w колебаний муфты не будет?

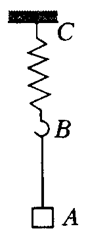
519. Груз А подвешен к пружине ВС с помощью нити АВ. Какова должна быть амплитуда колебаний груза, чтобы эти колебания были гармоническими? Масса груза m = 0,1 кг, жесткость пружины k = 1600 Н/м.

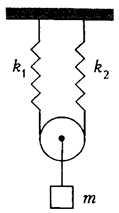
551. Груз массой m подвешен к двум пружинкам жесткостями k₁ и k₂ с помощью нити и блока. Найдите период малых колебаний груза. Нить и блок считать невесомыми.

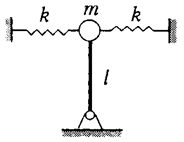
555. а) Легкий жесткий стержень длиной l с грузом массой m наверху закреплен шарнирно в нижней точке и удерживается в вертикальном положении двумя горизонтальными пружинами жесткостью k, скрепленными с его верхним концом. В направлении, перпендикулярном к пружинам, стержень двигаться не может. При какой массе груза вертикальное положение стержня перестанет быть устойчивым? б) Стальная спица длиной l заделана в пол так, что стоит вертикально. Если к ее верхнему концу приложить небольшую горизонтальную силу F, верхний конец спицы отклонится на величину а «l. Оцените, груз какой массы может выдержать, не согнувшись, спица на своем верхнем конце. Различием формы, которую принимает спица под действием на нее горизонтальной или вертикальной сил, пренебречь.

629. Шарик массой m подвешен на пружине жесткостью k (пружинный маятник). Точка подвеса пружины совершает вертикальные гармонические колебания с амплитудой A и частотой w. Как движется шарик при установившихся колебаниях?

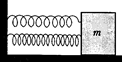
639. Две пружинки с жесткостями k₁ и k₂ присоединены каждая одним концом к вертикальной стене, другим — к грузу массой m, лежащему на горизонтальном столе. В начальный момент пружина с жесткостью k₁ растянута на величину l₁, а пружина с жесткостью k₂ сжата на величину l₂. Груз отпускают. Найдите амплитуду и период колебаний груза. Трением пренебречь.

641. Настенные часы с маятником имеют массу M = 5 кг. Масса груза на конце легкого маятника m = 150 г. Какая ошибка в показаниях часов накопится за сутки, если часы подвесить к потолку на двух длинных параллельных шнурах? Считать, что часы, прикрепленные к стене, идут точно.

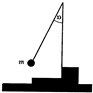
654. Штатив массой M стоит на гладком столе. К штативу на легкой нити длиной l прикреплен шарик массой m. Нить отклоняют на малый угол a и отпускают. Нарисуйте график зависимости скорости штатива от времени. Столкновения шарика с основанием штатива абсолютно упругие.

659. Небольшой станок массой m = 200 кг вибрирует при работе из-за неоднородности тяжелого маховика, вращающегося с угловой скоростью 600 об/с. Чтобы снизить вибрацию перекрытия в цехе, в котором установлен станок, под станину положили упругую прокладку толщиной h = 10 см из материала с модулем упругости Е = 3,1×10⁸ Н/м². Площадь основания станины S = 2 м². Приведет ли установка прокладки к уменьшению вибраций перекрытия?

663. Тяжелая тележка движется со скоростью v₀ по горизонтальной плоскости и въезжает на наклонную плоскость, составляющую угол a с горизонтом. Переход между плоскостями плавный. На тележке, на нити длиной l, висит шарик. Какова будет амплитуда колебаний шарика, когда тележка въедет на наклонную плоскость?

668. Через неподвижный блок перекинута невесомая нить. К одному концу нити прикреплен груз массой m₁. К другому концу на пружине жесткостью k подвешен груз массой m₂. Длина пружины в нерастянутом состоянии l₀. Найдите амплитуду колебаний, которые будет совершать груз m₂, когда систему предоставят самой себе. Качаний поперек нити нет.

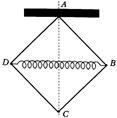
692. Конструкция, изображенная на рисунке, состоит из четырех легких жестких стержней длиной l каждый и легкой пружины длиной 2l. Стержни скреплены небольшими одинаковыми массивными шариками. В точке A система закреплена. В состоянии равновесия системы стержни образуют квадрат. Определите период малых колебаний системы, при которых точка C движется вдоль вертикали.

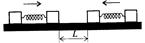
702. Две системы, каждая из которых состоит из двух одинаковых масс m, связанных пружинкой жесткостью k, движутся по гладкой горизонтальной поверхности навстречу друг другу с одинаковыми по величине скоростями v,. В некоторый момент времени расстояние между системами равно L. Определите время, через которое расстояние между теми же массами снова будет равно L. Столкновение систем считать абсолютно упругим.

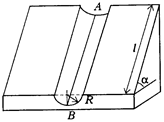
717. Маленький шарик скользит без трения по цилиндрическому желобу радиусом R, ось которого наклонена под углом j к горизонту; длина желоба l. Сколько раз шарик пересечет линию AB, если он начал свое движение вблизи точки A?

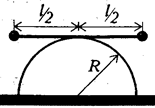
733. На полуцилиндре с радиусом основания R лежит гантелька длиной l. Найдите период малых колебаний гантельки.

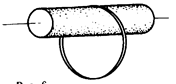
Ф751. На очень шероховатый цилиндр радиуса r, расположенный горизонтально, надет тонкий обруч радиуса R. Найти период колебаний обруча в вертикальной плоскости.

872. Длинные сани, скользящие по очень гладкому льду, въезжают на асфальт и останавливаются, не пройдя половины своей длины. После этого саням резким толчком сообщают первоначальную скорость, и они вновь останавливаются. Как относятся времена торможения в первом и во втором случаях? Как относятся пути торможения?

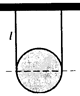
777. На невесомой нерастяжимой нити подвешен блок. Расстояние между точками подвеса нити равно диаметру блока; длина вертикальных участков нити равна l. Определите период малых колебаний системы в вертикальной плоскости, в которой лежит нить.

884(задача Н. Е. Жуковского). Жук ползет по жесткой (непрогибающейся) соломинке, опирающейся на гладкий пол и гладкую вертикальную стенку. Соломинка однородная, длина ее l, масса m, масса жука М (М» m). Соломинка образует угол a с горизонтом. Начальная скорость жука в верхней точке B была равна v₀. Как должен двигаться жук, чтобы соломинка оставалась неподвижной? Как зависит ускорение жука от пройденного им вдоль соломинки расстояния? За какое время жук доползет до нижней точки A? Сможет ли жук подняться по соломинке из точки A в точку B?

Ф964. Материальные точки образуют замкнутую систему. Между любыми двумя точками системы действует сила притяжения, равная F _ij = k×m_i×m_j× r _ij, где m_i, m_j — массы точек, | F _ij| — сила, действующая на точку i со стороны точки j, | r _ij| — расстояние между точками, k — постоянный коэффициент. В начальный момент все частицы покоятся. Докажите, что через некоторое время все точки столкнутся. Определите это время, если известны масса всей системы М = Sm_i, и коэффициент k.

А. Г. Самосват

Ф981. На груз массы М, висящий на пружине, кладут груз массы m, удерживая груз М в первоначальном положении, а затем грузы отпускают. Найти максимальную силу, действующую на груз m со стороны груза М.

П. И. Зубков

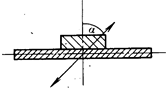
Ф1026. Горизонтальная площадка, на которой лежит брусок, вибрирует по гармоническому закону с частотой f = 10 Гц в направлении, составляющем угол a = 45° с вертикалью. Коэффициент трения бруска о площадку m = 0,5. При какой минимальной амплитуде вибраций брусок «поползет» по площадке?

Е. И. Бутиков

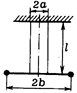
Ф1057. Гантель, состоящая из двух шариков массой m каждый, закрепленных на концах легкого стержня длиной 2b, подвешена в горизонтальном положении на двух нерастяжимых нитях длиной l, расстояние между которыми 2а. Найти период малых крутильных колебаний гантели.

М. М. Цыпин

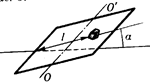
Ф1147*. На площадке, наклоненной под небольшим углом a к горизонту, на расстоянии l от ее нижнего края лежит маленький грузик, масса которого много меньше массы площадки. Площадка совершает гармонические колебания вдоль оси OO'; частота колебаний равна w, амплитуда — L. Коэффициент трения между грузиком и площадкой равен m. За какое время грузик свалится с площадки? (Считать, что это время много больше периода колебаний площадки.)

Ф1167. Длинный железнодорожный состав, двигаясь по инерции, въезжает на горку с углом a. Когда состав полностью остановился, на горке находилась половина его длины. Сколько времени прошло от начала подъема до остановки? Длина состава L, трением пренебречь.

А. И. Буздин

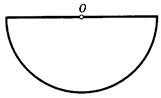
Ф1277. Из тонкой проволоки сделали замкнутую фигуру, изображенную на рисунке. Радиус полуокружности равен R. Где находится центр тяжести этой фигуры? Чему равен период малых колебаний относительно точки О?

А. Черноуцан

Ф1359. На гладком горизонтальном столе расположен пружинный маятник — тяжелый груз на легкой пружине, длина которой в свободном состоянии L = 50 см. Из-за небольшого вязкого трения о воздух колебания маятника медленно затухают — амплитуда уменьшается в 2 раза за 10 полных колебаний. Для поддержания амплитуды неизменной поступают следующим образом: свободный конец пружины быстро сдвигают на l = 1 мм навстречу грузу в тот момент, когда длина пружины минимальна, и возвращают в прежнее положение, когда она максимальна. Определите установившуюся амплитуду таких колебаний.

3. Рафаилов

Ф1454. Маятник состоит из жесткого невесомого стержня длиной l и закрепленного на его конце груза массой m. На груз нанесен электрический заряд Q. Заряд q противоположного знака укреплен над точкой подвеса на расстоянии d от нее. Чему равен период малых колебаний маятника? При какой величине заряда груза возможны такие колебания?

О. Шведов

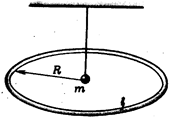
Ф1091. Подвешенный на нерастяжимой нити длиной l шарик с массой m и зарядом q находится в центре обруча, вдоль которого равномерно распределен заряд Q. Радиус обруча — R, заряды q и Q — одноименны. Определить частоту малых колебаний шарика, воспользовавшись формулой (1+x)^a = 1+ax (х«1).

Г. В. Григорьев

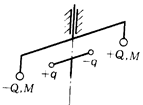
Ф1176. На невесомом коромысле длиной 2L, которое может вращаться без трения вокруг вертикальной оси, закреплены заряды +Q и —Q массой М каждый. Под коромыслом на продолжении оси вращения расположен маленький диполь — заряды +q и —q на расстоянии 2а друг от друга (a<<L). В начальный момент коромысло находится в состоянии устойчивого равновесия.

а) Диполь приводят во вращение с угловой скоростью w. При каких w коромысло будет «сопровождать» вращение диполя?

б) Диполь неподвижен. Найти период малых колебаний коромысла.

А. В. Андрианов

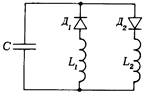
Ф800. Схема состоит из конденсатора емкости С, диодов Д₁ и Д₂, и катушек с индуктивностями L₁ и L₂ собранных, как показано на рисунке. Найти период колебаний напряжения на конденсаторе в этой схеме.

Г. Л. Коткин, Г. В. Меледин

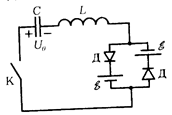
Ф1112. В схеме на рисунке при разомкнутом ключе К конденсатор заряжен до некоторого напряжения U₀. Ключ замыкают, и через какое-то время ток в цепи прекращается. Какова должна быть величина U₀ чтобы напряжение на конденсаторе установилось равным U = 1 В при изменившейся полярности пластин, если ЭДС каждой батареи в цепи 1 = 1,5 В? Диоды считать идеальными.

А. И. Киркинский

Ф1130. Колебательный контур состоит из вакуумного конденсатора емкостью С, расстояние между пластинами которого d, и катушки индуктивности. Собственная частота колебаний контура равна w₀. Какой будет собственная частота, если между пластинами конденсатора поместить свободную точечную частицу массой m, имеющую заряд q? Сила тяжести отсутствует. Краевыми эффектами и силой «электростатического изображения» пренебречь.

Д. А. Купцов

Ф1266. Две металлические сферы радиусом R каждая удалены друг от друга на большое расстояние и соединены друг с другом очень тонким проводником, в разрыв которого включена катушка индуктивностью L. На одну из сфер помещают электрический заряд. Через какое время заряд этой сферы уменьшится в два раза? Через какое время заряд снова станет таким же, как в первый момент?

А. Быцко

Ф1455. Конденсаторы, емкости которых С и 2С, заряжены каждый до напряжения U₀ и соединены последовательно «минусом» к «плюсу». К ним одновременно подключают две катушки: катушку индуктивностью L к конденсатору большей емкости, а катушку индуктивностью 2L к разноименным концам батареи конденсаторов. Найдите максимальный ток каждой из катушек. Через какое время после включения ток первой катушки станет максимальным?

А. Зильберман

Date: 2015-05-19; view: 2687; Нарушение авторских прав