
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Квантовый гармонический осциллятор
|
|
| v |
| Ev |
| x |
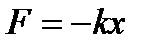 с собственной частотой колебаний
с собственной частотой колебаний  (где k и m - постоянные) и обладающая потенциальной энергией
(где k и m - постоянные) и обладающая потенциальной энергией 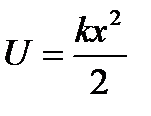 .
.
В квантовой физике из-за соотношения неопределенностей понятие силы теряет смысл и под гармоническим осциллятором понимают частицу массы m, обладающую потенциальной энергией U(х) такой же, как у классического осциллятора: 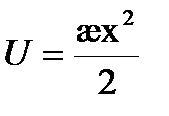 , где
, где
æ = const. Формально вводят 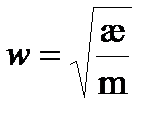 , которая не имеет физического смысла частоты колебаний. Тогда
, которая не имеет физического смысла частоты колебаний. Тогда 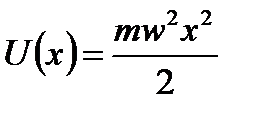 и уравнение Шредингера для стационарных состояний принимает вид:
и уравнение Шредингера для стационарных состояний принимает вид: 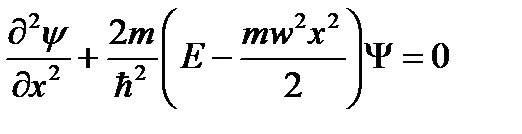 . Оно имеет решения (конечные, однозначные, непрерывные и гладкие), т.е.
. Оно имеет решения (конечные, однозначные, непрерывные и гладкие), т.е.  - функции при собственных значениях:
- функции при собственных значениях: 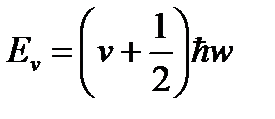 , где
, где
v = 0, 1, 2,... - квантовое число. 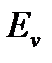 эквидистантны. Схема энергетических уровней:
эквидистантны. Схема энергетических уровней:
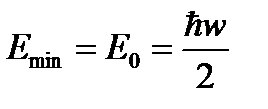
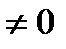 - нулевая энергия, что соответствует принципу неопределенности (частица не может лежать на дне параболической потенциальной ямы, т.к. не может иметь точной координаты).
- нулевая энергия, что соответствует принципу неопределенности (частица не может лежать на дне параболической потенциальной ямы, т.к. не может иметь точной координаты).
Доказано, что для квантового осциллятора возможны переходы лишь между соседними уровнями при которых v меняется на единицу 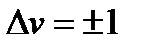 - правило отбора для квантового гармонического осциллятора. Каждый переход сопровождается испусканием (при уменьшении v) или поглощением (при увеличении v) кванта энергии
- правило отбора для квантового гармонического осциллятора. Каждый переход сопровождается испусканием (при уменьшении v) или поглощением (при увеличении v) кванта энергии 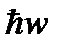 , т.е. здесь формальная величина
, т.е. здесь формальная величина 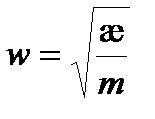 приобретает физический смысл.
приобретает физический смысл.
Неверно полагать, что осциллятор совершает колебания с частотой w. Следует гово-рить не о колебаниях, а о плотности распределения вероятности местонахождения частицы:

Классическая частица:
а) за пределы интервала выйти не может;
б) с наибольшей вероятностью (во времени) ее можно обнаружить в крайних точках, где ее скорость уменьшается до нуля, полная энергия E = U и она совершает поворот.
Квантовая частица:
а) может быть обнаружена за пределами интервала (- х; + х), в котором E<U.
б) может быть обнаружена в середине интервала с большей вероятностью чем по краям (особенно для v = 0).
в) с увеличением v квантовый осциллятор все более похож на классический (вероятность обнаружения частицы в центре интервала уменьшается, по краям – увеличивается).
| r |
| r0 |
| U |
| 0 |
Date: 2015-05-19; view: 593; Нарушение авторских прав