Экзаменационные задачи по курсу Квантовая теория

[Задача 1.] Найти оператор 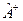, если

а) , ; , ;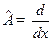

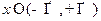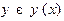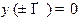б) , ; , .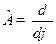

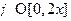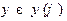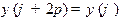Задача 2. Показать, что произвольный линейный оператор 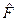может быть представлен в виде

; , .

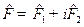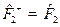[Задача 3.] Найти 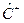, если 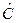- произведение эрмитовых операторов 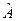и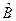

Задача 4. Решить уравнение 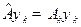для оператора

,

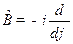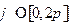
Задача 5. Для стационарного состояния вида

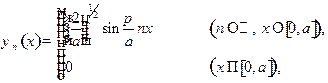
описывающего в одномерном случае частицу в бесконечно глубокой потенциальной яме ширины 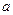, рассчитать средние значения величин, соответствующих операторам:

а)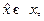

б)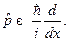

[Задача 6.] В 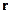- представлении (одномерная система) решить уравнение 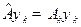для оператора 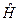в случае частицы в бесконечно глубокой потенциальной яме, ширины .

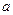[Задача 7.] Рассчитать коммутатор .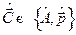

Задача 8. Найти коммутатор .

Задача 9. Для стационарного состояния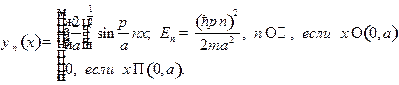

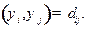
рассчитать 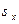и .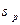

Экзаменационные вопросы по курсу "Квантовая теория".(минимум)

1. Принцип неопределенности.
2. Полный набор динамических переменных.
3. Постулаты квантовой механики.
4. Волновая функция и ее свойства.
5. Принцип суперпозиции состояний.
6. Операторы в квантовой механике.
7. Собственные функции и собственные значения эрмитовых операторов. Случай дискретного (и непрерывного)* спектра.
8. Операторы координаты 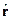, импульса 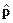, момента импульса 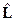, энергии .
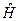9. Волновое уравнение
10. Оператор Гамильтона различных систем.
11. Решение волнового уравнения в случае свободной материальной точки
12. Собственный механический момент (спин).

Экзаменационные задачи по курсу "Квантовая теория".(минимум)

Задача 1. Найти оператор 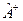, если

а) , ; , ;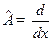

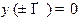б) , ; , .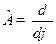

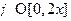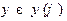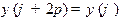Задача 2. Найти 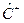, если 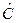- произведение эрмитовых операторов 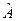и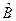

В сферических координатах 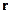- представления найти собственную функцию оператора .

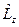Задача 3. В 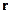- представлении (одномерная система) решить уравнение 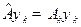для оператора 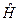в случае частицы в бесконечно глубокой потенциальной яме, ширины .

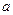Задача 4. Рассчитать коммутатор .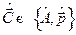

Решения задач по курсу "Квантовая теория"

[Задача 1.] Найти оператор 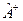, если

а) , ; , ;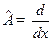

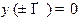б) , ; , .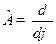

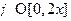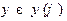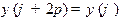Решение. Подставляя явный вид 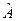в правую часть 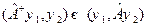и проводя интегрирование по частям, получим

а) ,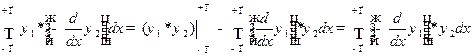

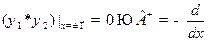
б) ,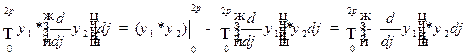

.

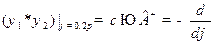Здесь использовано обращение функци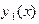й и 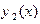в нуль на бесконечности в случае (а) и условие периодичности функци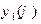и и 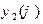в случае (б). В обоих случаях оператор 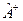не совпадает с оператором .

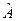Задача 2. Показать, что произвольный линейный оператор 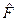может быть представлен в виде

; , .

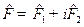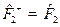Решение. Легко видеть, что справедливо разложение 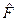на сумму

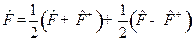
двух операторов, первый из которых является эрмитовым:

, ,

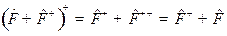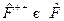а второй – антиэрмитовым:

.

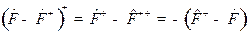С их помощью будем иметь

; , ;

, .

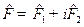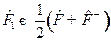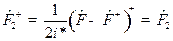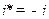Всякая линейная комбинация эрмитовых операторов с вещественными коэффициентами есть Эрмитов оператор. Произведение двух эрмитовых операторов не обязательно эрмитово.

[Задача 3.] Найти 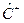, если 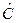- произведение эрмитовых операторов 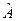и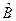

Решение. Из определения 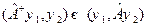имеем

;

, /

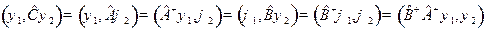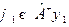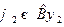Отсюда с учетом эрмитовост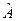и и 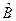найдем

.

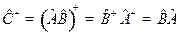Легко видеть, что в общем случае .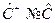

Задача 4. Решить уравнение (7.3) для оператора

,

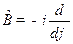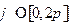
Решение. Из решения задачи 3(б) и равенств

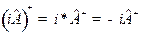
найдем

,

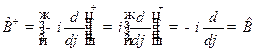т.е. рассматриваемый оператор 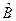Эрмитов, а его собственные значения вещественны. Уравнение (7.3) примет вид

.

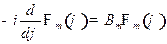Решая его, найдем

.

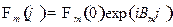Из условия периодичности (см. задачу 3(б))

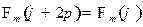
вытекает равенство

,

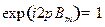из которого получаем ограничение

;

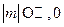
Из дискретности и невырожденности спектра следует, что после нормировки (8.4) функции 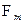будут обладать свойством (8.3).

Запишем условие нормировки (8.4) в виде

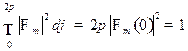
В общем случае постоянный множитель есть комплексное число, однако ввиду всегда допустимого введения произвольного фазового множителя

,

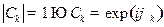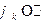
будем предполагать вещественность константы 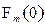. Это дает

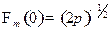
Окончательно запишем

;

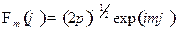Задача 9. Для стационарного состояния вида

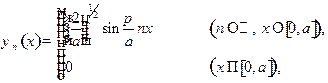
описывающего в одномерном случае частицу в бесконечно глубокой потенциальной яме ширины 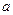, рассчитать средние значения величин, соответствующих операторам:

а)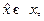

б)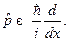

Решение. а) По определению ,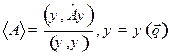

запишем

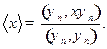
Расчет числителя (12.3) дает

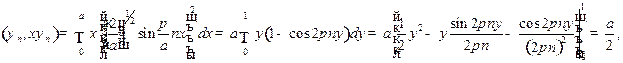
где использованы соотношения

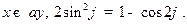
Аналогичным образом для знаменателя (12.3) получим

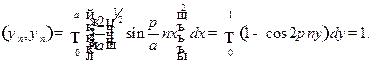
Следовательно, для 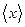будем иметь

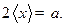
б) Учитывая свойство (7.2) и определение (12.2), запишем

.

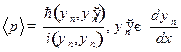Расчет числителя (12.4) дает

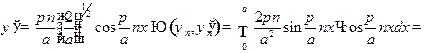
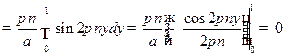
таким образом, для 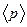будем иметь

[Задача 6.] В - представлении (одномерная система) решить уравнение (7.3) для оператора 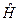в случае частицы в бесконечно глубокой потенциальной яме, ширины .

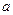Решение. В случае бесконечно глубокой ямы по определению имеем

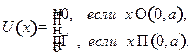
Интересующее нас решение ищем на отрезке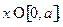

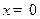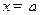Поскольку в точках и потенциальная энергия частицы обращается в бесконечность, вероятность преодоления бесконечного барьера и попадания за пределы области (17.2) равна нулю. Оказавшись в области (17.2), частица все время будет находиться в ней. Из формул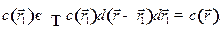

и

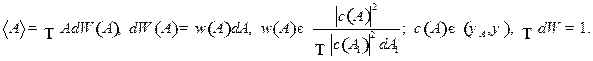
следуют соотношения

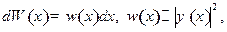
где 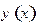- волновая функция 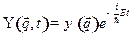, удовлетворяющая стационарному уравнению Шредингера

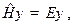
совпадающему с уравнением (13.1) или (13.2) (в зависимости от характера спектра), т.е. функция 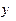, удовлетворяющая (17.5), есть собственная функция 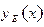оператора 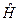, соответствующая собственному значению 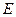. Из сказанного вытекают граничные условия 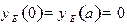, накладываемые на решение уравнения (17.5).

Таким образом, приходим к задаче

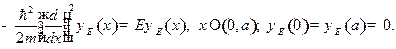
Отсюда следует:

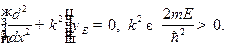
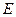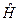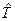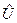Положительность собственного значения оператора вытекает из положительности и . Решение уравнения (17.7) представимо в виде суперпозиции двух элементарных состояний, которые на языке 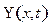(17.3) интерпретируются как волны де Броля, распространяющиеся в противоположных направлениях оси :

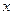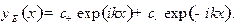
Подстановка (17.8) в граничные условия (17.6) приводит к системе однородных уравнений

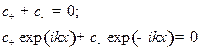
для неизвестных коэффициентов 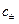. Критерий существования тривиального решения этой системы

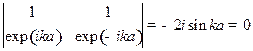
дает условие квантования

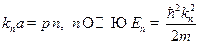
собственного значения (17.5). Это означает, что обладает дискретным спектром, а уравнение (17.5) эквивалентно (7.3). Вводя согласно (17.9) обозначения

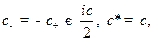
где 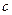- пока неизвестная вещественная (в силу наличия у 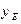произвольного фазового множителя (10.1) это всегда возможно) константа, для функции (17.8) будем иметь

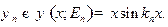
Поскольку собственные функции оператора 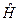с дискретным спектром квадратично интегрируемы, условие нормировки имеет вид

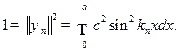
Отсюда с учетом решения задачи 12 находим

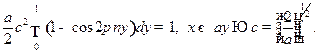
Подставляя найденное значение константы в (17.10), запишем решение задачи в окончательной форме

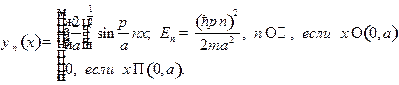
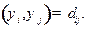
[Задача 7.] Рассчитать коммутатор .

Решение. Для нахождения явного вида оператора 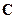необходимо рассмотреть результат его действия на произвольную функцию 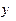. Используя (13.6), (14.2) и определение 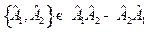, запишем

.

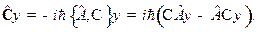
Задача 8. Найти коммутатор .

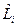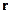Решение. Используя (19.2) и вид в - представлении

,

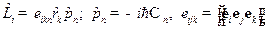запишем

.

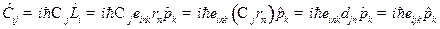Date: 2015-05-18; view: 845; Нарушение авторских прав