
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

A.3. Стационарная теория возмущений в случае близких энергетических уровней
|
|
Пусть у нас два близких уровня, а остальные уровни хорошо удовлетворяют критерию (5).
Пусть близкие уровни - это уровни i=1,2. Близость уровней определяется из критерия (5).
Модификация теории возмущений состоит в том, чтобы в качестве нулевого приближения для 1 и 2 состояния подобрать такие функции 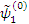 и
и 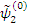 , которые обращали бы в ноль
, которые обращали бы в ноль 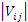 - числитель критерия (5).
- числитель критерия (5).
По определению:
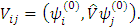
Мы рассмотрим набор
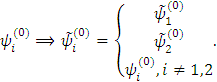
Очевидно, что
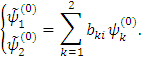
Распишем:
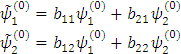
Рассмотрим свойства невозмущенной функции:
Они удовлетворяют ЗШЛ:
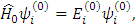
где  - невозмущенный оператор.
- невозмущенный оператор.
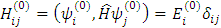 (6)
(6)
Эта матрица имеет диагональный вид, т. к. мы рассматриваем матричные элементы на собственных функциях этого оператора.
Мы ввели 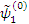 и
и 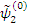 для того, чтобы ввести такой матричный элемент, чтобы он
для того, чтобы ввести такой матричный элемент, чтобы он
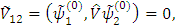
тогда (5) будет для 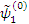 и
и 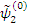 давать 0 и теория возмущений будет работать.
давать 0 и теория возмущений будет работать.
Таким образом, мы ввели новый возмущенный базис 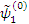 и
и 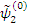 . В этом новом базисе мы должны диаганализовать
. В этом новом базисе мы должны диаганализовать 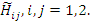
Искомое преобразование является унитарным, так как оно не нарушает условия нормировки. Надо подобрать коэффициенты 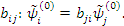
Используем
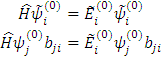
Но
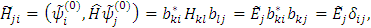
или в матричном виде
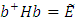
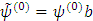
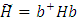
Из свойства ортонормированности найдем свойства коэффициентов 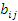
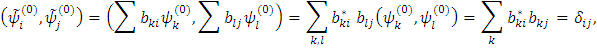
т.е.
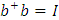
Это унитарное преобразование, оно сохраняет нормировку.
Запишем ЗШЛ для модифицированных функций.
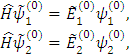
тогда подставим явно 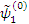 и
и 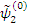
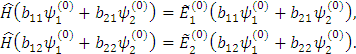
Рассмотрим случай i=1, умножим левую и правую части этого уравнения скалярно на 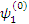 и
и 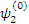 , тогда имеем:
, тогда имеем:
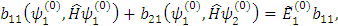
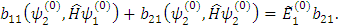
Введем обозначения:
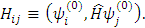
Перепишем эти уравнения в виде
 (7)
(7)
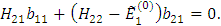
Система линейных однородных уравнений. Она имеет нетривиальное решение только при det=0.
Обозначим
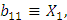
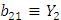
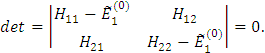
Имеем решение
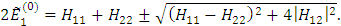
При i=2, то по аналогии
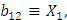
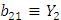
и обозначив
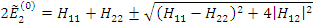
получаем
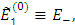
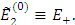
Во втором случае решение аналогично первому. Однако мы приписываем одному знак +, а другому -.
Имеем тогда уровни энергии:
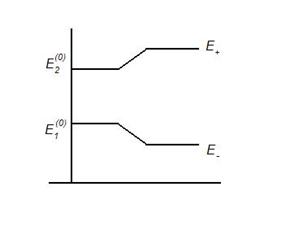
Перейдем к системе (7). Из нее имеем
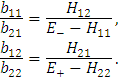
Кроме этого используем соотношение
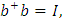
т.е. имеем нормировку
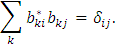
Рассмотрим i=j=1 (и аналогично i=j=2)

Введем обозначение:
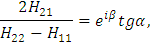
где α и β – вспомогательные углы, определяемые через матричные элементы H 12, H 11 и H 22.
Тогда коэффициенты b имеем в виде
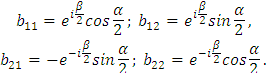
Таким образом, при 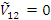 теория возмущений срабатывает для двух близких уровней. Теперь в качестве нулевого приближения берут:
теория возмущений срабатывает для двух близких уровней. Теперь в качестве нулевого приближения берут:
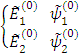
Модификация касалась только этих дух близких состояний. Остальные состояния не модифицировались, т.к. они сразу удовлетворяли критерию.
Теперь 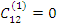 и
и 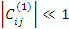 – теория возмущения работает.
– теория возмущения работает.
Экзаменационные вопросы по курсу "Квантовая теория".
- Экспериментальные основы квантовой механики.
- Классическое и квантовое описание системы.
- Принцип неопределенности.
- Полный набор динамических переменных.
- Постулаты квантовой механики.
- Роль классической механики в квантовой механике.
- Волновая функция и ее свойства.
- Принцип суперпозиции состояний.
- Понятие о теории представлений.
- Операторы в квантовой механике.
- Собственные функции и собственные значения эрмитовых операторов. Случай дискретного (и непрерывного)* спектра.
- Среднее значение измеряемой величины.
- Вероятность результатов измерения.
- Коммутативность операторов и одновременная измеримость физических величин. (1/2*)
- Операторы координаты
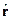 , импульса
, импульса 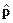 , момента импульса
, момента импульса 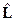 , энергии
, энергии 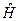 .
. - Решение задачи на собственные функции и собственные значения для оператора
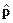 .
. - Решение задачи на собственные функции и собственные значения для оператора
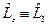 .
. - Вычисление коммутаторов, содержащих операторы
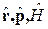 (и
(и 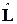 *).
*). - Волновое уравнение
- Производная оператора по времени
- Интегралы движения в кв. механике.
- Флуктуации физических величин. (1/2*)
- Неравенство Гайзенберга. (1/2*)
- Оператор Гамильтона различных систем.
- Стационарное состояние различных систем
- Решение волнового уравнения в случае свободной материальной точки
- Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы.
- Собственный механический момент (спин).
- * Операторы
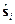 и
и 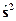 и их свойства.
и их свойства. - Спиновая переменная волновой функции
- Матрицы Паули (и их свойства *).
- Принцип тождественности.
- Стационарная теория возмущений (нулевое и первое приближения).
Date: 2015-05-18; view: 688; Нарушение авторских прав