Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы

В случае бесконечно глубокой ямы по определению имеем

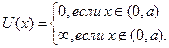
Интересующее нас решение ищем на отрезке

.

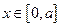Поскольку в точках x=0 и x=a потенциальная энергия частица обращается в бесконечность, вероятность преодоления бесконечного барьера и попадания за пределы области 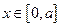равна нулю. Оказавшись в этой области частица все время будет находиться в ней. Из определения волновой функции следует

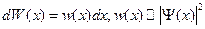
где в.ф. удовлетворяет стационарному уравнению Шредингера

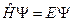
совпадающему с определением оператора 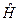, т.е. функция 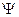есть собственная функция этого оператора, соответствующая собственному значению Е. Из сказанного вытекают граничные условия 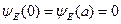, накладываемые на решение уравнения.

Таким образом, приходим к задаче

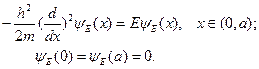
От сюда следует:

(*)

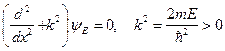Положительность собственного значения Е оператора 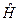вытекает из положительности 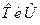. Решение уравнения (*) представимо в виде супепозиции двух элементарных сосотояний, которые на языке 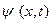интерпритируются как волны де Бройля, распространяющиеся в противоположных направлениях оси x:

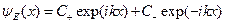
Подстановка решения в граничные условия приводит к системе однородных уравнений

(**)

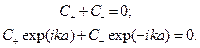Для неизвестных коэффициентов С_{+/_.} Критерий существования нетривиального решения данной системы

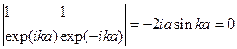
дает условие квантования

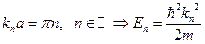
собственного значения Е. Это означает, что 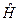обладает дискретным спектром. Вводя согласно (**) обозначения

где С - неизвестная пока вещественная (в силу наличия у в.ф. произвольного фазового множителя) константа, для искомой в.ф. будем иметь

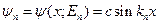
Поскольку собственные функции оператора 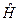с дискретным спектром квадратично интегрируемы, условие нормировки имеет вид

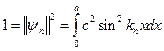
От сюда, интегрируя, получаем

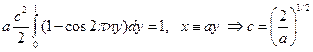
Подставляя найденное значение константы, запишем решение задачи в окончательной форме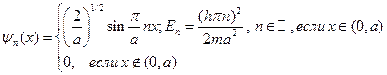

[§ 28.] Собственный механический момент (спин)

Рассмотрим Na. У него есть желтая линия. Возникает при переходе с уровня 3p на 3s.

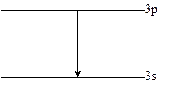
Первоначально ее длина была 5892

Было обнаружено, что эта линия расщепляется на две: дублет.

Возникла идея расщепления уровня 3p на два, тогда можно объяснить возникновение двух линий.

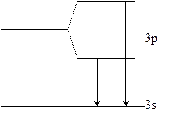
Их длины: 5896 и 5890 .

В 1925 г. Была предложена гипотеза спина, т. е. собственного механического момента.

У электрона спиновое число s= .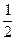

Впоследствии Паули ввел спин в теорию.

Если имеем одну частицу, то она характеризуется орбитальным квантовым числом .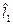

Составная частица (атом) состоит из многих микрочастиц. Можно рассматривать эту составную частицу вцелом и приписать ей момент 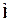, который описывает орбитальное движение частицы как целого.

Энергетический уровень этой составной частицы в некоторых полях будет зависеть от орбитальных моментов микрочастиц .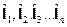

Эти моменты являются внутренним свойством этой составной частицы.

Можно рассматривать 2 момента:

1) 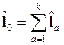. Этот момент описывает внутреннее движение частицы (относительно центра инерции)

2) Частица сама движется по некоторой траектории.

У частицы есть еще квантовое число 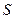, характеризующее собственный механический момент.

Вводят оператор собственного механического момента:

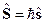
По аналогии

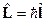
Спин – внутреннее свойство частицы. Его смысл – у частицы есть внутренний параметр, который реагирует на вращение координат независимо от места положения частицы.

Date: 2015-05-18; view: 467; Нарушение авторских прав