Интегралы движения в квантовой механике

В классической механик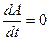е , где , тогда A – интеграл движения.

В квантовой механике, чтобы величина , которой ставится в соответствие оператор 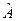, была интегралом движения нужно, чтобы .

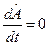Для того чтобы физическая величина сохранялась, необходимо и достаточно, чтобы .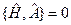

1. т. к. 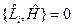, то -значение момента импульса сохраняется, т. е. является интегралом движения.

2. 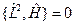. 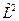- интеграл движения.

3. 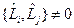. Отсюда следует. Что различные компоненты момента импульса одновременно не измеримы. А измерима только одна проекция .

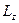4. 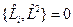. Квадрат импульса одновременно измерим с любой компонентой момента импульса.

5. 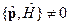, тогда импульс не является интегралом движения.

§22. Флуктуации физических величин (1/2*)

Пусть есть 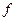- физическая величина, которая при измерении с вероятностью W_i дает величину , тогда мы можем говорить о среднем 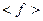и о дисперсии , где

.

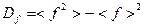Мы вводили флуктуацию

,

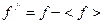отклонение величины 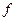от ее среднего значения.

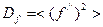
Перенесем все это на язык квантовой механики, т. к. физической величине 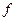мы ставим в соответствие .

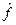Можно показать, что .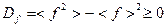

Неравенство Коши-Шварца: Оно справедливо и для функциональных пространств, в том числе и для гильбертова пространства, которое рассматривается в квантовой механике.

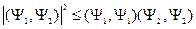
Для двух векторов оно имеет вид

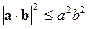
имеет смысл тот, что .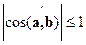

, .

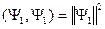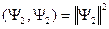Теперь если обозначить 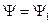, , 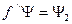тогда будем также рассматривать статистическое усреднение 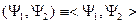. Отсюда получим из неравенства Коши-Шварца:

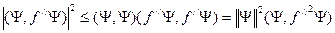
Теперь если определить 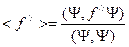. К тому же по определению из 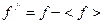имеем 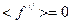, тогда 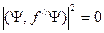. Из этого следует, что

.

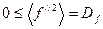В случае квантовой механики 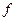заменяем на 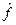, тогда

.

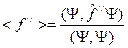Задача. Для стационарного состояния частицы в бесконечно глубокой потенциальной яме найти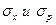

Date: 2015-05-18; view: 1226; Нарушение авторских прав