
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Операторы координаты , импульса , момента импульса , энергии
|
|
Будем использовать координатное представление (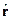 -представление). Будем рассматривать систему из одной материальной точки. Действие
-представление). Будем рассматривать систему из одной материальной точки. Действие 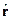 сводитсяк умножению на вектор
сводитсяк умножению на вектор 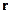 , т. е.
, т. е. 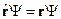 (это определение действия оператора
(это определение действия оператора 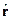 ).
).
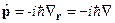
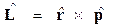
Здесь строго соблюдается последовательность операторов при раскрытии векторного произведения, например, первая компонента:
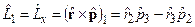 ,
,
однако для частного случая декартовых координат порядок операторов не существенен.
Оператор энергии или гамильтониан 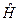 :
:
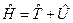 ,
,
здесь 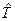 - оператор кинетической энергии,
- оператор кинетической энергии, 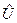 - оператор потенциальной энергии. Для одной материальной точки гамильтониан имеет вид:
- оператор потенциальной энергии. Для одной материальной точки гамильтониан имеет вид:
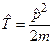
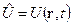
Переменная t – признак внешнего нестационарного поля.
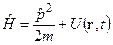
Тут присутствует 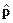 и
и 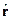 , но
, но 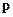 и
и 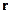 одновременно неизмеримы, тогда потенциальная и кинетическая энергия в квантовой механике не могут быть одновременно измеримыми. В квантовой механике существует понятие “энергия частицы”, но порознь вводить энергию нельзя, иначе либо
одновременно неизмеримы, тогда потенциальная и кинетическая энергия в квантовой механике не могут быть одновременно измеримыми. В квантовой механике существует понятие “энергия частицы”, но порознь вводить энергию нельзя, иначе либо 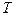 , либо
, либо 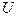 оказываются неизвестными.
оказываются неизвестными.
§16. Решение задачи на собственные функции и собственные значения для оператора 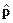
Оператор импульса – оператор с непрерывным спектром собственных значений.
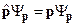 (16.1)
(16.1)
Мы рассматриваем координатное представление, тогда 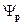 - функция координат.
- функция координат.
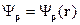
Оператор 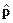 векторный, он имеет три компоненты:
векторный, он имеет три компоненты:
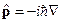
Например:
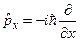 (16.2)
(16.2)
Тогда уравнение (16.1) разбивается на три независимых члена, т.к. операторы 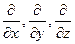 коммутируют. Существует утверждение, что если
коммутируют. Существует утверждение, что если 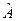 можно представить в виде суммы коммутирующих операторов:
можно представить в виде суммы коммутирующих операторов:
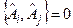 ,
, 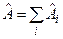 ,
,
то задача на собственные функции и собственные значения 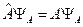 распадается на подзадачи этих коммутаторов:
распадается на подзадачи этих коммутаторов:
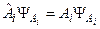
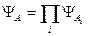
Для задачи (16.1) имеем:
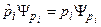 ,
,
где i принимает значения 1,2,3
Решим случай i=1, тогда
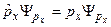 (16.3)
(16.3)
Подставляем (16.2) в (16.3) и временно опустим индекс px у 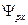 , тогда имеем
, тогда имеем
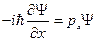
т.к. 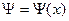 - функция одной переменной, то:
- функция одной переменной, то:
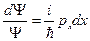
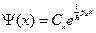
здесь 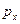 - число, собственное значение.
- число, собственное значение.
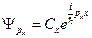
При решении задачи получили, что p имеет непрерывный спектр на всей числовой оси. Т. е. 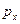 - не квантуется. Найдем
- не квантуется. Найдем 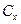 . Используем условие ортонормированности:
. Используем условие ортонормированности:
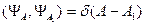
В нашем случае:
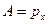 ,
, 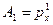
Тогда:
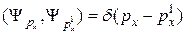 (16.4)
(16.4)
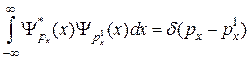 .
.
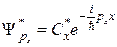 .
.
Обозначим 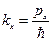 .
.
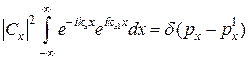 .
.
Тогда
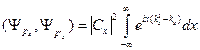
Интеграл дает с точностью до множителя 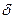 - функцию, поскольку:
- функцию, поскольку:
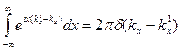
Используем следующее свойство 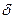 -функции:
-функции:
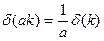 .
.
В нашем случае получим
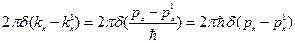 ,
,
тогда
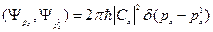 (16.5)
(16.5)
Сравнивая (16.5) и (16.4) получим:
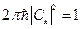
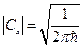
В связи с тем, что волновые функции в квантовой механике определены с точностью до фазового множителя, то
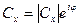 .
.
Фаза 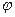 точно не определена, и ее можно отнести к самой волновой функции. Такая неоднозначность принципиальна и не может быть устранена, однако она несущественна, так как не отражается ни на каких физических величинах. Таким образом:
точно не определена, и ее можно отнести к самой волновой функции. Такая неоднозначность принципиальна и не может быть устранена, однако она несущественна, так как не отражается ни на каких физических величинах. Таким образом: 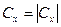 . Мы получили
. Мы получили
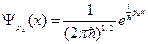
Теперь запишем 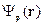 - для трёх мерного случая:
- для трёх мерного случая:
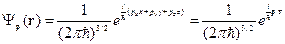 (16.6)
(16.6)
Функция (16.6) удовлетворяет условию нормировки (16.4).
В импульсном представлении: 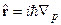
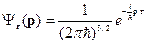
Date: 2015-05-18; view: 1020; Нарушение авторских прав