Вычисление коммутаторов, содержащих операторы (и *)

Для оператора :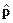

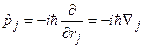
Найдем 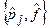, где 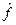- есть функция 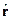и 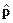, т.е. 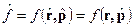- координатное представление.

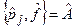
Подействуем этим коммутатором на некоторую произвольную функцию :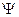

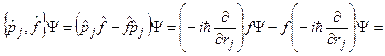
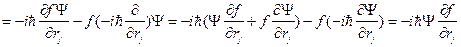
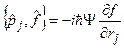(18.1)

Аналогичный результат для оператора 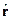в импульсном представлении:

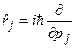
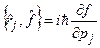, (18.2)

Здесь .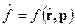

Рассмотрим частные случаи формул (18.1) и (18.2):

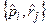
1. 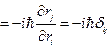, здесь 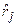играет роль функции .

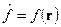2.

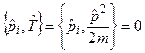
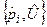
3. 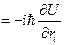, здесь 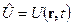потенциальная энергия - функция координат и времени.

3a.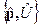

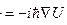
4.

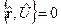
5. 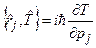, здесь импульсное представление, таким образом .

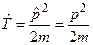5a. 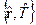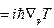.Для одной материальной точки 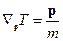, тогда:

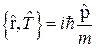
6. 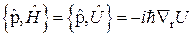- координатное представление.

7. 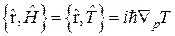- импульсное представление.

Рассмотрим соотношение для оператора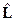

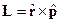
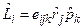
Используем дополнительное соотношение:

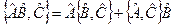
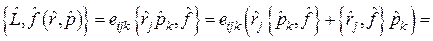{используем (18.1) и (18.2): 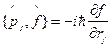, 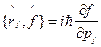} 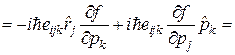{ 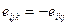, тогда второе слагаемое 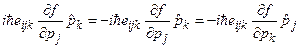} 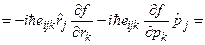{в классической математике измерение компонента вектора при бесконечно малом повороте:

,

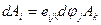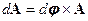
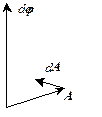
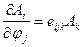это отношение справедливо и в квантовой теории поля:

}={ }={ ,

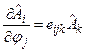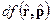
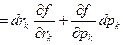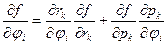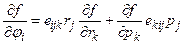. В общем случае импульс и координата не коммутируют, тогда функция координат и импульсов и импульс, координата и функция координат и импульсов не коммутируют. Если f – функция скалярная, тогда она не меняется при вращении. В этом случае, чтобы 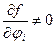, то f – векторная функция.} 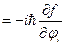(где f есть компонента некоторой векторной величины, т. е.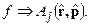

Тогда перепишем 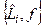в виде :

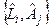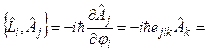{меняем местами индексы}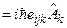

Тогда для любой векторной функции имеем:

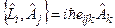
Здесь вместо 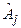можно подставить, например,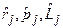

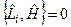- коммутатор 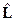с любым скаляром равен нулю.

Получим:

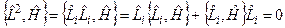
Date: 2015-05-18; view: 2038; Нарушение авторских прав