Вероятность результатов измерения

Пусть 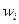- вероятность того, что при измерении величины для системы, находящейся в состоянии 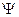мы получим результат 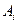. Если система находится в состоянии 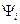, то величина 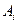при измерении выходит с вероятностью равной 1:

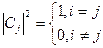
В общем случае;

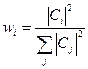
Если полная производная оператора 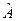удовлетворяет равенству

,

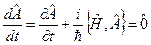то собственная функция оператора 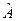описывает состояние системы.

Для непрерывного спектра, вероятность того, что результаты измерения величины A для системы, находящейся в состоянии 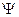, лежит в интервале от 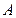до 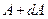, определяется следующим выражением:

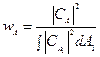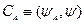, (13.1)

или плотность вероятности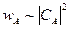

§14. Коммутативность операторов и одновременная измеримость физических величин (1/2*)

Введем понятие коммутатора

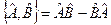
Если мы имеем 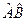, то предполагается, что на некоторую функцию 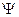сначала действует 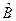, а потом на все действует 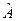. Если 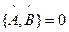, то операторы 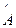и 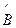коммутативны. Причем физические величины, соответствующие этим операторам одновременно измеримы. Или говорят, что эти операторы имеют общий базис. То есть, все собственные функции этих операторов можно выбрать общими. Разложим 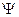по базису.

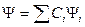
Подействуем на 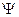коммутатором:

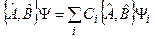
Используем то, что 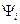образуют общий базис :

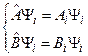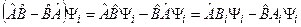
Числа с оператором коммутируют (т. к. операторы эрмитовы), тогда:

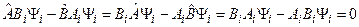
В результате получаем:

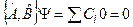
То есть, если физические величины одновременно измеримы, то коммутатор соответствующих им операторов равен нулю. Также справедливо обратное утверждение - если коммутатор операторов обращается в нуль, то физические величины соответствующие этим операторам одновременно измеримы. Докажем это утверждение:

Пусть 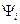собственная функция оператора 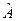, т.е. 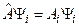. Подставляем ее в коммутатор:

Тогда получим 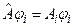. Мы рассматриваем невырожденный спектр. Это значит, что одному собственному значению соответствует единственная собственная функция. Разница между функциям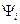и и 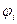только до константы. Пусть эта константа - 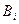, тогда 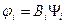. Но 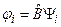, тогда 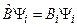. Мы получили, что функция 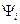удовлетворяет задаче на собственные функции и собственные значения для оператора 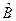. Это можно показать для любой собственной функции оператора 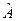. Тогда из коммутативности операторов 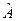и 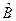следует общность базисов.

Величины и 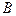, которым соответствуют коммутирующие операторы, могут быть одновременно измеримы и, следовательно, могут образовывать полный набор динамических переменных. Полный набор динамических переменных полностью задает состояние системы. Но операторы 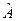и 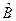должны быть независимы.

Date: 2015-05-18; view: 507; Нарушение авторских прав