Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решение задачи на собственные функции и собственные значения для оператора
|
|
Если в классической механике рассматривать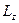 
, то
.
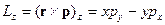Если полученному выражению поставить в соответствие оператор в квантовой механике, то он может быть записан в виде:
,
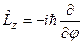где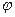 
- угол поворота вокруг оси 
.
Рассмотрим задачу на собственные функции и собственные значения для оператора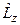 
:
,
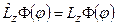
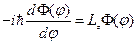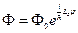
Мы накладываем на функцию 
условие периодичности, т. к. угол 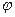меняется от 
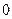до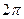 
, т. е.:
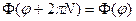
Используя данное ограничение можно записать:
,
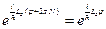
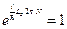
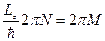
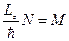где N и M целые числа, значит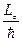 
тоже должно быть целым:
,
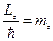
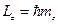где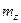 
- целое безразмерное число. Из условия периодичности получили квантованность проекции орбитального момента на ось z. Спектр собственных значений оператора 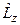дискретный. Так как 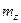целое число, то функция приобретает индекс:
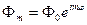
Найдем константу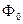 
. Запишем условие нормировки 
:
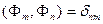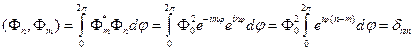
При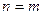 
интеграл дает 
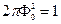. В результате получаем выражение для 
:
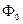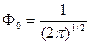
Тогда имеем для уравнения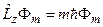 
собственную волновую функцию
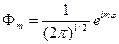
Таким образом, спектр собственных значений оператора 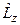дискретный, а собственные функции нормируемые.
Date: 2015-05-18; view: 695; Нарушение авторских прав