Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Постулаты квантовой механики. Часто выделяют 4 постулата:
|
|
Часто выделяют 4 постулата:
1) Постулат о волновой функции.
Каждой системе (состоянию кв.-мех. системы) может быть поставлена в соответствие волновая функция динамических переменных (из полного набора) и времени, полностью описывающей состояние системы.
Динамические переменные одновременно измеримы.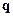 
- n – мерный вектор динамических переменных; функция динамических переменных и времени 
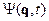- описывает эволюцию квантово-механических систем. классической механике задание 2n динамических переменных полностью определяет состояние системы через функцию Гамильтона. В квантово-механической системе описывается эволюция системы через 
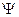- функцию от n динамических переменных.
2) О связи физических величин и объектов математики (операторов).
Каждой физической величине (наблюдаемой) ставится в соответствие оператор: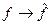 
3) Связь между результатами измерения физической величины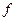 
и значением оператора 
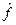(т. е. решением математических задач)
Пусть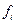 
- значение физической величины 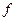, которое получено в результате измерения системы, находящейся в i -том квантовом состоянии.
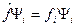
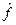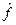является одним из собственных значений оператора . Это задача на собственные функции и собственные значения. Задача определяет собственные значения , соответствующие и определяет собственные функции 
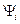, соответствующие собственным значениям . Если собственные значения образуют дискретное множество, то говорят о дискретном спектре. Если собственные значения образуют непрерывное множество, то спектр непрерывный.
4) Определение среднего значения физической величины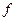
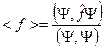
Здесь введено понятие скалярного произведения для функций из гильбертова пространства. Гильбертово пространство – это пространство квадратично интегрируемых функций (нормируемых функций). Если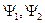 
- квадратично интегрируемые функции, тогда:
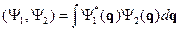
Это определение для 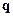- декартовых переменных. Для перехода к другой системе координат вводится якобиан перехода. Значок «*» означает комплексное сопряжение.
Это аналог длины в векторном пространстве.
Date: 2015-05-18; view: 638; Нарушение авторских прав