
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Аналогично
|
|
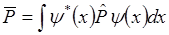
Второй постулат квантовой механики:
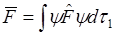
где 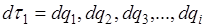 .- обобщённые координаты.
.- обобщённые координаты.
Например: 1) 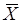 линейного гармонического осциллятора в нормальном состоянии. Нормированная волновая функция этого состояния известна.
линейного гармонического осциллятора в нормальном состоянии. Нормированная волновая функция этого состояния известна.
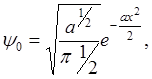
где 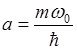
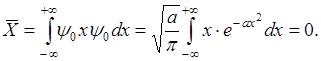
все интегралы вида 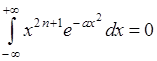 вследствие нечётности подынтегральной
вследствие нечётности подынтегральной
функции.
2) Определим P
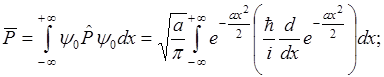
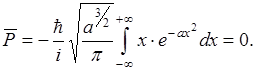
Как и в классической механике, 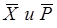 в этом случае равны нулю, что и следовало ожидать из соображений симметрии функции
в этом случае равны нулю, что и следовало ожидать из соображений симметрии функции 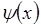 относительно х.
относительно х.
3) Вычислим средние значения кинетической и потенциальной энергии:
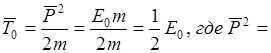
т. е. средняя потенциальная энергия равна средней кинетической, как и в классической механике.
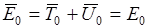
И как и следовало ожидать, поскольку нулевое состояние есть состояние с определённой энергией.
Условия возможности одновременного измерения разных
механических величин.
Согласно одному из основных постулатов квантовой механики, механической величине можно приписывать определённое значение только в том случае, когда это значение является собственным значением 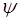 - функции, описывающей состояние, в котором находится система.
- функции, описывающей состояние, в котором находится система.
При каких условиях две или несколько механических могут иметь одновременно определённые значения.
Две механические величины F и G имеют определённые значения, если состояние описывается функцией 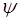 , являющейся собственной функцией того и другого оператора, т. е. общей собственной функцией.
, являющейся собственной функцией того и другого оператора, т. е. общей собственной функцией.
Например: 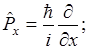
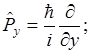
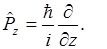
Собственные функции этих операторов удовлетворяют уровням.
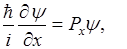
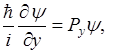
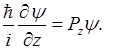
Где 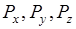 - собственные значения операторов.
- собственные значения операторов.
Функция 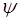 равная
равная
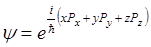
удовлетворяет всем этим трем уравнениям, т.е. является общей собственной функцией операторов 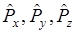 . Это показывает, что проекции количества движения на все три оси координат могут иметь одновременно определенные значения.
. Это показывает, что проекции количества движения на все три оси координат могут иметь одновременно определенные значения.
ТЕОРЕМА: Если операторы имеют общие собственные функции, то такие операторы коммутируют.
Пусть 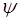 общей собственной функцией операторов
общей собственной функцией операторов 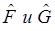 .
.
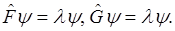
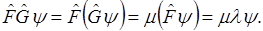

Следовательно, 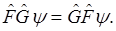
Обратная теорема: Если операторы коммутируют, то они имеют общие собственные функции.
Динамические переменные 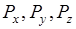 имеют общую собственную функцию, следовательно, их операторы коммутируют.
имеют общую собственную функцию, следовательно, их операторы коммутируют.
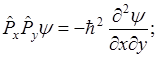
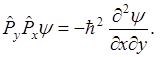
Откуда следует 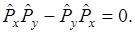
Аналогично 
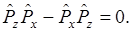
Координатам соответствующая другой координате составляющая импульса также коммутируют.
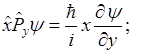
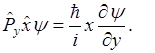
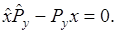
Но координата и соответствующая ей составляющая импульса не коммутируют,
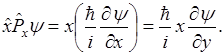
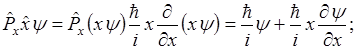
т.е. 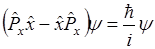
или 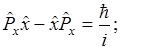
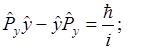
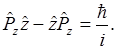
Не могут иметь определенные значения координаты m соответствующие mm составляющие количества движения, либо одна из них имеет определенное значение m тогда другая будет неопределенна.
Составляющие момента импульса не коммутируют:
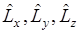
Соотношения неопределенностей.
В классической механике записаны так 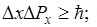 .
. 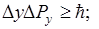
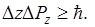
Т.е. на опыте, исходя на основе физических соображений, не можем одновременно получить абсолютно точные значения. Неопределенности обусловлены не совершенством наших измерений, а самой природой материи.
Квантовая механика приводить к неизбежности этих неопределенностей.
Неопределенности или неточности характеризуются квадратным корнем из среднего квадрата отклонения:
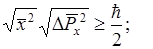
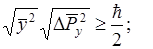
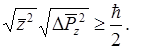
Они указывают верхний предел точности, который может быть достигнут при одновременном измерении координат m импульсов; произведение неточностей не может
быть меньше 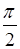
Свободная частица.
Одна частица, движущаяся в отсутствие действия сил в направлении, которое мы примем за ось X. Т.к. силы отсутствуют, то U=const мы можем принять ее равной нулю. Функция Гамильтона в классической механике состоит из одной кинетической энергии
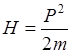
при выбранной оси координат x: 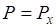 , оператор импульса будет
, оператор импульса будет
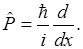
Оператор Гамильтона:

Уравнение Шредингера
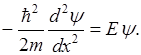
Частные решения этого уравнения, таковы 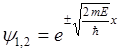
Эти условия удовлетворяют стандартным условиям конечности m непрерывности во всем пространстве при любых положительных значениях E: E>0.
Спектр собственных значений энергии в данном случае сплошной, в отличие от дискретного спектра.
Движение в центральном поле.
Оператор момента количества движения.
Движение в поле центральных сил. Важную роль играет в квантовой механике оператор момента количества движения.
В декартовых координатах:
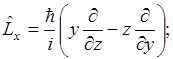
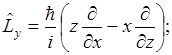
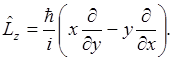
Теперь мы должны перейти в этой главе к сферическим координатам:
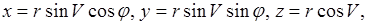
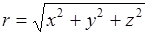
Напишем полный дифференциал 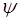 как функция x, у, z.
как функция x, у, z.
. 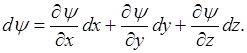
Переход к сферическим координатам, пологая, что r и V остаются постоянными, а изменяется то 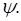
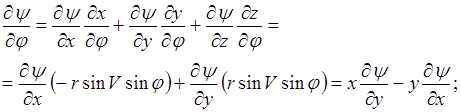
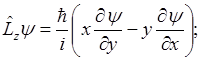
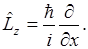
Аналогично выводится 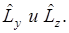
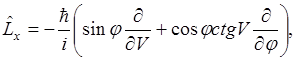
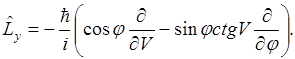
Операторы 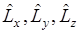 некоммутирующие операторы, поэтому определить можно одну компоненту, а две другие не определяются.
некоммутирующие операторы, поэтому определить можно одну компоненту, а две другие не определяются.
Оператор квадрата момента количества движения

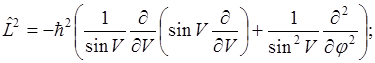
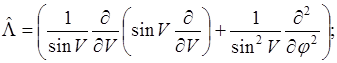
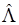 - оператор Лежандра.
- оператор Лежандра. 
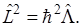
Каждый из операторов коммутирует с оператором 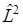 .
.

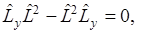
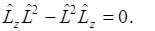
Оператор квадрата момента импульса имеет общие собственные функции с операторами каждой из его проекций.
Законы сохранения в центрально симметричном поле.
Оператор энергии полярных координатах:
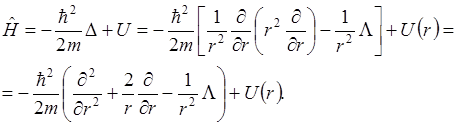
Вводится оператор радиального момента:
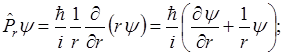
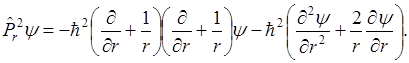
Если принять во внимание, что 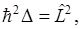 то
то 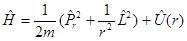 .
.
Оператор любой составляющей момента количества движения коммутирует с 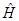 .
.
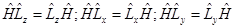 .
.
Это означает, что численное значение момента количества движения сохраняется во времени. 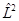 и
и 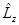 коммутируют с
коммутируют с 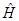 , следовательно все три оператора
, следовательно все три оператора 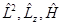 имеют общие собственные функции.
имеют общие собственные функции.
А поэтому численное значение момента количества движения, одна из его проекций и энергия могут одновременно определенные значения.
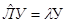 , где У - шаровая функция.
, где У - шаровая функция. 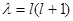 .
.
Шаровыми функциями называются шаровые полиномы (одновременные), удовлетворяющие уравнению Лапласа 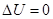 или в декартовых координатах
или в декартовых координатах
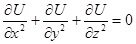
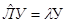 в раскрытом виде
в раскрытом виде
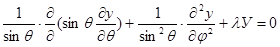
В сферических координатах
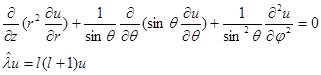
Где l есть квантовое число момента количества движения.
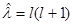 - собственное значение квадрата момента количества движения.
- собственное значение квадрата момента количества движения.
 т.е.
т.е. 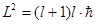
тогда момент количества движения 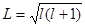 принимает собственные значения
принимает собственные значения 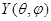 - собственная функция оператора.
- собственная функция оператора.
Собственные функции и собственные значения оператора проекции момента количества движения.
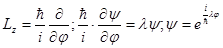
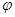 - циклическая переменная, то условие однозначности решения:
- циклическая переменная, то условие однозначности решения:
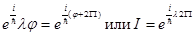 , это будет только в том случае, если
, это будет только в том случае, если 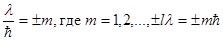 , т.е. при измерении z-составляющей момента количества движения должны получаться числа, являющиеся целыми кратными
, т.е. при измерении z-составляющей момента количества движения должны получаться числа, являющиеся целыми кратными  .
.
m – магнитное квантовое число.
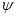 - собственная функция.
- собственная функция.
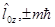 - собственные значения.
- собственные значения.
Различным значениям l, l=0,1,2,3,…,(n-1) соответствуют различные состояния s,p,d,f,…
| Состояние | l | m | 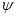 -функция -функция
| L | Lz | Lx | Ly |
| s | |||||||
| p | 
| 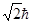
| 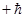
| Неопр. | Неопр. | ||
| p | 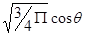
| 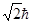
| Неопр. | Неопр. | |||
| p | -1 | 
| 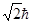
| 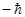
| Неопр. | Неопр. |
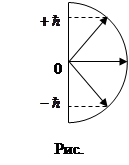
Волновые функции нормированы. Для каждого l имеется (2l+1) значений проекции момента импульса на ось z, которые являются целыми кратными  .
.
В теории Бора все три проекции 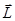 строго определены. На рисунке изображено пространственное квантование в состоянии P (1=1). Оператор
строго определены. На рисунке изображено пространственное квантование в состоянии P (1=1). Оператор 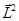 имеет в этом состоянии три собственные функции:
имеет в этом состоянии три собственные функции:
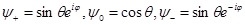 .
.
Всем трем собственным функциям соответствует только одно собственное значение L2, равное 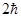 . Поэтому в состоянии P имеет место трехкратное вырождение. Вследствие вырождения состояние должно описываться линейной комбинацией трех функций
. Поэтому в состоянии P имеет место трехкратное вырождение. Вследствие вырождения состояние должно описываться линейной комбинацией трех функций 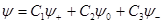 .
.
Все направления равновероятны. Всегда имеется отличная от 0 вероятность найти частицу на сфере с радиусом равным единице 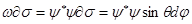 .
.
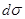 - элемент поверхности сферы r =1
- элемент поверхности сферы r =1
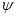 -функции приведены в таблицах при различных 1 и m.
-функции приведены в таблицах при различных 1 и m.
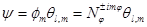
 - нормирующий множитель.
- нормирующий множитель.
 - азимутальная функция, зависит только от азимутального числа
- азимутальная функция, зависит только от азимутального числа 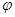 .
.
Эта функция соответствует бегущей по окружности волны и отвечает равномерному вращению электрона вокруг ядра, т.е. волна распространяющаяся в 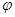 -том направлении.
-том направлении.
Из условия нормировки:
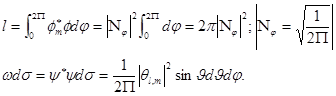
Исчез множитель от 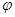
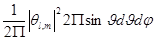 - вероятность найти частицу в любом месте сферы между кругами широт от
- вероятность найти частицу в любом месте сферы между кругами широт от 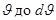 . Так как,
. Так как, 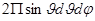 площадь сферического пояса между этими кругами.
площадь сферического пояса между этими кругами.
Вероятность, отнесенная к единице площади сферы,
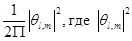 - эта функция и характеризует распределение частиц на сфере по широте.
- эта функция и характеризует распределение частиц на сфере по широте.
| m | 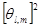
| 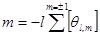
| |
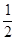
| 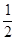
| ||

| 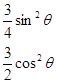
| 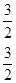
|
 |
Полярности диаграммы плотностей вероятности
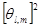 при
при 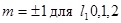 . Принято электронное облако (орбиталь) графически изображать контуром, ограничивающим область, в которой вероятность обнаружения электрона составляет 0,9.
. Принято электронное облако (орбиталь) графически изображать контуром, ограничивающим область, в которой вероятность обнаружения электрона составляет 0,9.
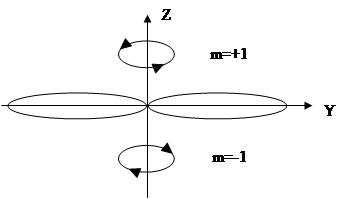 В состоянии l=0, m=0, E0=0, сферическая симметрия в распределении заряда электрона
В состоянии l=0, m=0, E0=0, сферическая симметрия в распределении заряда электрона
S-состояние; 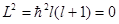 .
.
Покоящаяся частица может с равной вероятностью в любом месте сферической поверхности радиуса a, т.е. все положения равновероятны. Направление 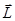 не зависит от угла
не зависит от угла 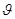 , классического аналога нет.
, классического аналога нет.
P-состояние: 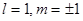
График надо вращать вокруг оси z.
При 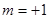 правое вращение, при
правое вращение, при 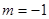 левое вращение (
левое вращение (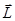 антипараллелен оси z), при m=+ 1 параллелен.
антипараллелен оси z), при m=+ 1 параллелен.
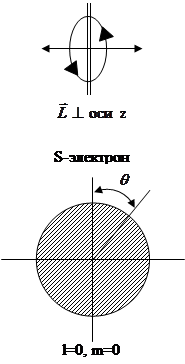
 l=1,m=0 наиболее вероятная орбита та, которая лежит в плоскости, проходящей через ось z.
l=1,m=0 наиболее вероятная орбита та, которая лежит в плоскости, проходящей через ось z.
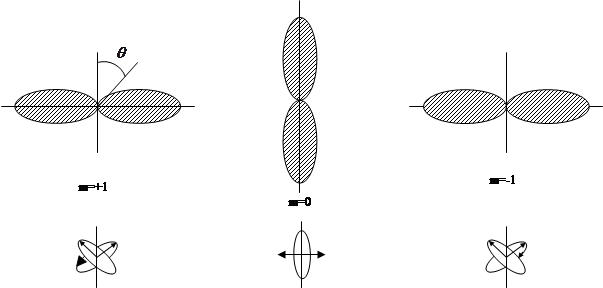
Во всех случаях наблюдается размытость электронного облака.
Существуют фотографии электронного облака для различных состояний водородоподобного атома.
Уравнение Шредингера для атома водорода.
В сферической системе координат для электрона:
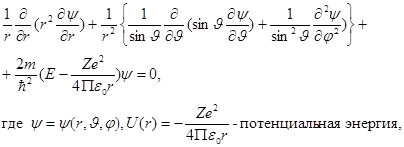
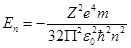 - собственное значение энергии электрона в атоме, n=1,2,3,…
- собственное значение энергии электрона в атоме, n=1,2,3,…
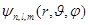 -определяется тремя параметрами;
-определяется тремя параметрами;
n – главное квантовое число, l – побочное квантовое число, m – магнитное квантовое число.
Вероятность 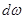 того, что электрон находится в области, ограниченной элементом объема dv1, взятого в окрестности точки с координатами
того, что электрон находится в области, ограниченной элементом объема dv1, взятого в окрестности точки с координатами 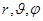 определяется
определяется
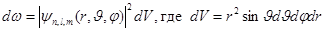 (в сферических координатах).
(в сферических координатах).
В состоянии s(l=0, m=0) волновая функция сферически симметрична (т.е. не зависит от углов (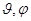 )).
)).
Нормированные собственные 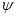 -функции, отвечающие за 1s-состояние (основному) и 2s-состоянию, имеют вид:
-функции, отвечающие за 1s-состояние (основному) и 2s-состоянию, имеют вид:
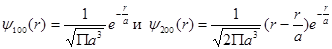
или в атомных единицах
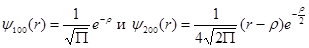
где в качестве единицы измерения длины выбран радиус первой боровской орбиты
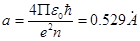
При таком выборе единицы длины расстояния осей ядра  будет выражаться в безразмерных величинах.
будет выражаться в безразмерных величинах.
В s-состоянии вероятность 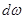 найти электрон в интервале (r,r+dr) одинакова по всем направлениям и определяется формулой
найти электрон в интервале (r,r+dr) одинакова по всем направлениям и определяется формулой
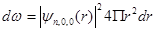
Момент импульса L и магнитный момент P, обусловлены орбитальным движением электрона:

где l – орбитальное квантовое число l=(0,1,2,3,…,(n-1)),
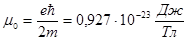
Проекция момента импульса Lz и магнитного момента Pz на направление внешнего магнитного поля:
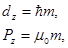
где m – магнитное квантовое число (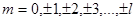 ).
).
Гиромагнитные отношения для орбитальных магнитного момента P и момента импульса L
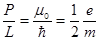
Момент импульса s и магнитный момент 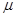 , обусловлены спином электрона
, обусловлены спином электрона
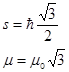
Проекции спиновых моментов импульса Sz и магнитного момента 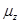 на направление внешнего магнитного поля
на направление внешнего магнитного поля
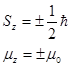
Проекции Sz и 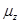 могут принимать только два значения.
могут принимать только два значения.
Гиромагнитное отношение для спиновых магнитного и механического моментов
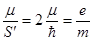
Распределение электронов по состояниям в атоме записывается с помощью спектроскопических символов:
| Значение орбитального числа l | ||||||||
| Спектрографический символ | s | p | d | f | g | h | i | k |
Электронная конфигурация записывается следующим образом:
2p – (n =2, l =1); 2p2 – (электронов в атоме ровно 2m и т.д.)
Принцип Паули: в атоме не может находиться два и более электронов, характеризуемых одинаковым набором четырех квантовых чисел: n, l, m, ms (где ms – спиновое магнитное квантовое число: 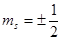 ).
).
Оператор Лапласа в сферических координатах:
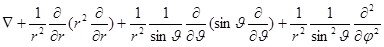
Ze – заряд ядра. Сила, связывающая электроны с ядром на расстояниях порядка атомных размеров (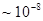 см) есть кулоновская сила притяжения. Соответствующая ей потенциальная энергия
см) есть кулоновская сила притяжения. Соответствующая ей потенциальная энергия
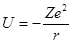
Для низшего энергетического состояния l =0 и оно полной сферической симметрией, так что функция 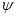 будет зависеть только от радиуса r и не будет зависеть от углов
будет зависеть только от радиуса r и не будет зависеть от углов 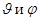 . Поэтому члены, содержащие производные по
. Поэтому члены, содержащие производные по 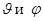 в операторе Лапласа, равны нулю и уравнение Шредингера принимает вид:
в операторе Лапласа, равны нулю и уравнение Шредингера принимает вид:
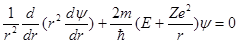
Обозначим 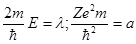
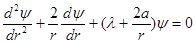
простейшее решение этого уравнения, имеющее конечное значение при r =0 и стремящееся к нулю при 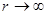 есть
есть
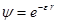
Действительно, имеем, прежде всего
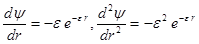
подставляем в выше написанное уравнение, и после сокращения на
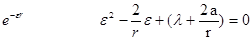
это соотношение должно иметь место при любом r, вследствие чего оба двучлена, взятые в скобки, должны равняться нулю, каждый в отдельности, т.е.
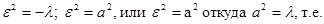
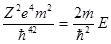 ,
,
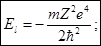
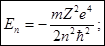
Сравнивая с формулой Бора для бальмеровых уровней энергии мы видим, что El, есть не что иное, как первый бальмеров уровень, соответствующий главному квантовому числу n= 1, l= 0, оно символически обозначается ls.
Z=1 и иногда энергия El водородного атома в нормальном состоянии, с обратным знаком, это и будет энергия ионизации атома водорода.
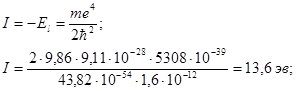
хорошее совпадение с экспериментальными данными.
Вычислим теперь вероятность электрона в элементе объема 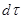 . Обозначим через N нормирующий множитель.
. Обозначим через N нормирующий множитель.
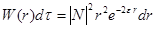 , где
, где
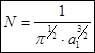
Постоянная 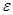 имеет размерность см-1.
имеет размерность см-1.
Введем новую постоянную 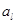 , связанную с
, связанную с 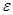 отношением:
отношением: 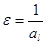
тогда: 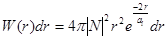
плотность вероятности W(r) обращается в нуль при 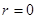 и асимптотически стремится к нулю при
и асимптотически стремится к нулю при 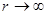 . Таким образом, имеется определенная вероятность найти электрон на любом расстоянии от ядра – между 0 и
. Таким образом, имеется определенная вероятность найти электрон на любом расстоянии от ядра – между 0 и 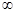 . Эта вероятность достигает максимума на расстоянии: продифференцируем последнее уравнение и приравняем к нулю, и после сокращения на
. Эта вероятность достигает максимума на расстоянии: продифференцируем последнее уравнение и приравняем к нулю, и после сокращения на 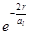
получим 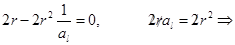
откуда 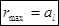 , где
, где 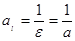
где 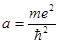 ; находим
; находим 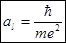 ;
;
С таким выражением встречались в теории Бора: n= 1, Z= 1
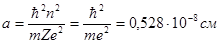 ;
;
это радиус первой водородной орбиты. Азимутальное квантовое число теории Бора
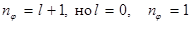
и здесь состояние ls характеризуется сферической симметрией, так что распределение вероятности представляет собой сферическое «облако», а не плоский образ, соответствующий «орбите». Заряд электрона представляют на всех графиках размазанный по всему пространству в виде облака.
Уравнение Шредингера
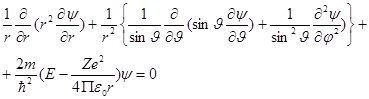
следует решать по методу разделения переменных, полагая
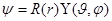
Умножая исходное уравнение на 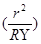 получаем:
получаем:
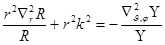
Так как слева стоит величина, зависящая только от r, справа – только от углов 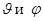 , это равенство может иметь место только в том случае, когда и левая, и правая части равны по отдельности некоторой величине
, это равенство может иметь место только в том случае, когда и левая, и правая части равны по отдельности некоторой величине 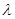 , называемой постоянной разделения.
, называемой постоянной разделения.
Для радиальной: 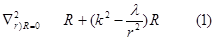
Для угловой: 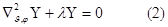
Полагая 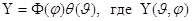
ее разделяют по сферическим углам:
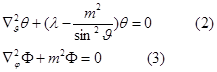
Частные производные заменяются полными дифференциалами.
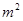 - постоянная разделения.
- постоянная разделения.
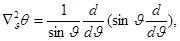
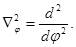
Каждая из функций 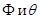 зависит только от одной переменной.
зависит только от одной переменной.
Таким образом, для определения собственных значений энергии 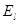 и соответствующих им собственных значений функций
и соответствующих им собственных значений функций 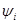 получим три уравнения:
получим три уравнения:
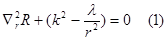
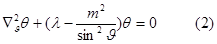
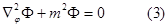
нормировка производится для каждой из функций по отдельности.
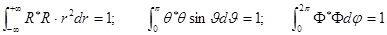
Частное решение для азимутальной функции: 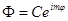 ,
,
либо 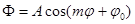 .
.
Волновая функция должна удовлетворять условию однозначности, 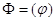 необходимо наложить условие периодичности
необходимо наложить условие периодичности 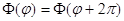 , из которого следует
, из которого следует
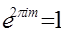 ,
,
где 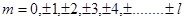 .
.
из условия нормировки 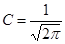
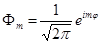
m – магнитное квантовое число, собственные значения его известны.
Решение второго уравнения:
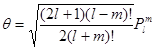
l – орбитальное квантовое число, l = 0,1,2,3,…, n -1
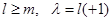
квантовое число характеризует собственное значение 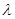 оператора
оператора 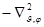 , входящего в квантовое операторное выражение функции Гамильтона
, входящего в квантовое операторное выражение функции Гамильтона
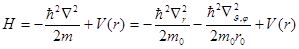 .
.
Сравнивая с классической функцией Гамильтона
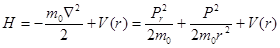 ,
,
где 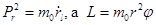 , видим, что оператору
, видим, что оператору 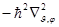 в классическом случае соответствует квадрат момента количества движения
в классическом случае соответствует квадрат момента количества движения 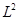 , а оператору
, а оператору 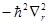 - квадрат радиального импульса
- квадрат радиального импульса 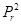 .
.
В классической механике момент количества движения 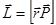 , а момент внешних сил
, а момент внешних сил 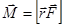 , и изменения
, и изменения 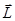
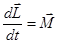
В случае центральных сил 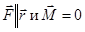 , тогда
, тогда 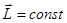 закон сохранения количества движения.
закон сохранения количества движения.
Чтобы обобщить классическое выражение на квантовый случай, надо заменить 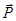 оператором импульса
оператором импульса
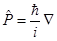 ,
,
тогда 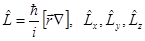 - не коммутируемые операторы.
- не коммутируемые операторы.
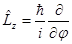 ;
;
действуя 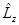 на шаровую функцию
на шаровую функцию
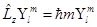 ;
;
m – характеризует проекцию момента количества движения на ось z.
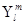 - собственная функция операторов
- собственная функция операторов 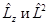
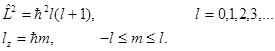
При 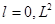 обращается в нуль, в то время по классической теории это величина не может вообще обращаться в нуль. Состояние
обращается в нуль, в то время по классической теории это величина не может вообще обращаться в нуль. Состояние 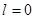 не имеет классического аналога. Механический момент атома, находящегося в наинизшем состоянии, обращается в нуль. Экспериментальные данные из области спектроскопии подтверждают этот квантово-механический результат.
не имеет классического аналога. Механический момент атома, находящегося в наинизшем состоянии, обращается в нуль. Экспериментальные данные из области спектроскопии подтверждают этот квантово-механический результат.
Решение простейших задач в сферических координатах.
Ротатор – представляет собой частицу, движущуюся по сфере радиуса 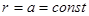 . Это задача – движение под действием центральных сил, когда потенциальная энергия постоянна, и можно положить равной нулю.
. Это задача – движение под действием центральных сил, когда потенциальная энергия постоянна, и можно положить равной нулю. 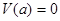 .
.
Угловая часть описывается шаровыми функциями, а для определения радиальной функции берем уравнение
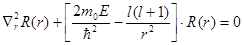 ,
,
где 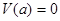 , подставим
, подставим 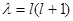 .
.
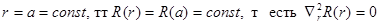 .
.
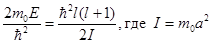 - момент инерции.
- момент инерции.
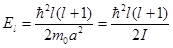
Энергия ротатора зависит от орбитального квантового числа, магнитное квантовое число, характеризующее проекцию момента 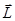 на ось Z, в выражение
на ось Z, в выражение 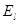 не входит. Собственному значению
не входит. Собственному значению 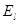 соответствуют собственные функции
соответствуют собственные функции 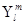 , зависящие от m. m может меняться от
, зависящие от m. m может меняться от 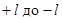 , каждому значению энергии
, каждому значению энергии 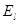 будут соответствовать (2 l+1) собственных функций, описывающих состояния ротатора, отличающиеся лишь ориентацией момента
будут соответствовать (2 l+1) собственных функций, описывающих состояния ротатора, отличающиеся лишь ориентацией момента 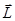 относительно оси Z, то есть уровень энергии
относительно оси Z, то есть уровень энергии 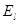 является
является 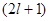 -кратно вырожденным.
-кратно вырожденным.
 При l= 0 имеем однократно вырожденный уровень, который называется просто невырожденным.
При l= 0 имеем однократно вырожденный уровень, который называется просто невырожденным.
Состояния: l= 0, 1, 2, 3, 4 …
s, p, d, f, g и так далее.
Рассмотрим S и P состояния ротатора.
В S-состоянии 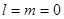 , собственная функция
, собственная функция 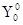 , соответствующая нулевому собственному значению энергии
, соответствующая нулевому собственному значению энергии 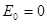 , будет равна
, будет равна  .
.
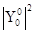 -квадрат модуля – плотность вероятности
-квадрат модуля – плотность вероятности 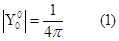
В P-состоянии 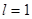 , квантовое число m может принимать три значения: -1, 0, +1, следовательно, собственному значению энергии
, квантовое число m может принимать три значения: -1, 0, +1, следовательно, собственному значению энергии 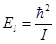 соответствуют три собственные функции:
соответствуют три собственные функции:
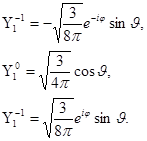
Плотности вероятности:

Величина  представляет вероятность обнаружить частицу на сфере постоянного радиуса в области углов
представляет вероятность обнаружить частицу на сфере постоянного радиуса в области углов  .
.
Поскольку квадрат модуля не зависит от угла, вероятность обнаружить частицу в одном и том же интервале углов становится одинаковой. В силу этого произведение соответствует плотности вероятности обнаружить частицу между углами.
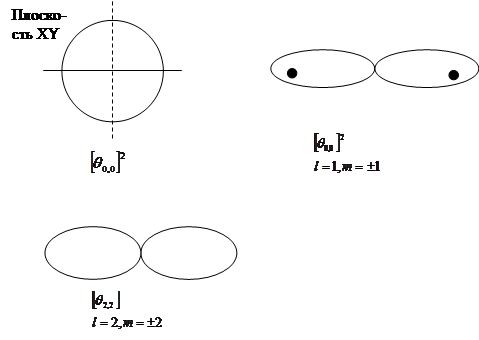
Графически распределение плотности вероятности (1), (2), (3) представлены на рисунке:
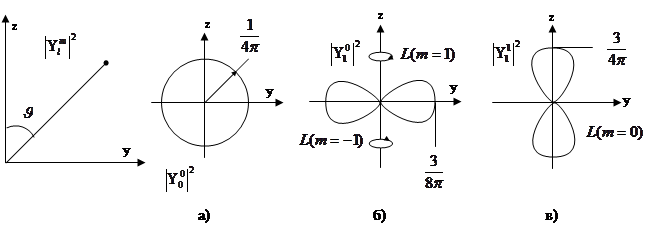
Чтобы поучить полную картину нужно вращать вокруг оси Z. Рис а) и из (1) направление момента 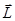 относительно оси Z для ротатора в состоянии S не зависит от угла
относительно оси Z для ротатора в состоянии S не зависит от угла 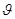 , так как
, так как 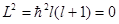 . Покоящаяся же материальная точка может с равной вероятностью находиться в любом месте сферической поверхности радиуса
. Покоящаяся же материальная точка может с равной вероятностью находиться в любом месте сферической поверхности радиуса 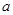 , то есть все положения ротатора возможны и равноправны. Классического аналога S-состояние не имеет.
, то есть все положения ротатора возможны и равноправны. Классического аналога S-состояние не имеет.
Из (2) и рис. б) следует, что наиболее вероятной из всех траекторий ротатора в P-состоянии с 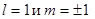 является та, которая расположена в плоскости (xy), причем состояния с
является та, которая расположена в плоскости (xy), причем состояния с 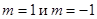 отличаются одно от другого направлением оси вращения: при
отличаются одно от другого направлением оси вращения: при 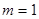 ротатор обладает правым вращением (момент количества движения
ротатор обладает правым вращением (момент количества движения 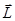 параллелен оси Z), а при
параллелен оси Z), а при 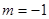 - левым (момент
- левым (момент 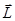 антипараллелен оси Z).
антипараллелен оси Z).
При l=1 и m =0 наиболее вероятной орбитой ротатора является та орбита, которая лежит в плоскости, проходящей через ось Z (рис. в)). При этом момент направлен перпендикулярно оси Z.
Аналогичным образом можно исследовать состояния с l = 2 (пять значений 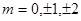 ), с l =3 и так далее.
), с l =3 и так далее.
Во всех случаях наблюдается размытость электронного облака.
Существуют фотографии электронного облака для различных состояний водородоподобного атома.
Date: 2015-05-18; view: 1070; Нарушение авторских прав