
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные положения квантовой механики. 2 page
|
|
В классической механике гармонический осциллятор может иметь любую произвольную полную энергию Е, а его максимальное смещение от положения равновесия (амплитуда колебаний) xo ограничено и связано с энергией соотношением 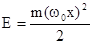 . В квантовой механике для анализа характеристик особенностей движения гармонического осциллятора необходимо решить уравнение Шредингера с данной потенциальной энергией
. В квантовой механике для анализа характеристик особенностей движения гармонического осциллятора необходимо решить уравнение Шредингера с данной потенциальной энергией

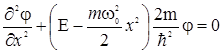 . (1.20)
. (1.20)
Решение такого дифференциального уравнения в аналитическом виде достаточно сложно, но качественные особенности аналогичны предыдущим случаям. На рисунке 7 представлены графики получаемого решения и возможные значения энергий.
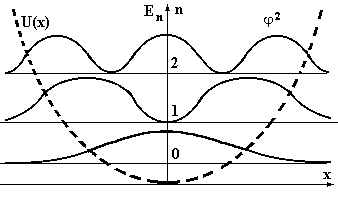
Рис.7. Графики вероятности нахождения гармонического осциллятора для n = 0, 1, 2. Горизонтальные, тонкие линии показывают значения энергий состояний (энергетическая диаграмма или уровни возможных энергий системы), толстые линии показывают j2, пунктирная – вид потенциала.
Возможные значения для полной энергии при решении определяются формулой
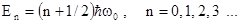 . (1.21)
. (1.21)
Из этой формулы видно, что полная энергия гармонического осциллятора тоже квантована, а ее минимальная величина при n = 0 отлична от нуля, также как и в предыдущих случаях. Наличие энергии нулевых колебаний – это чисто квантовый эффект, он говорит о том, даже в области нулевой потенциальной энергии у частицы имеется ненулевая кинетическая энергия и ненулевой импульс. Это означает, что микрочастица постоянно двигается и не может находиться в абсолютном покое.
Подтверждение наличия нулевых колебаний было получено в экспериментах по рассеиванию света в кристаллах. Согласно классической теории, при абсолютном нуле температуры по Кельвину колебаний атомов около узлов кристаллической решетки и соответственно рассеивания света, вызываемого этими колебаниями, не должно быть. Эксперименты показывают, что интенсивность рассеянного света при уменьшении температуры уменьшается, но даже при температурах очень близких к абсолютному нулю интенсивность рассеянного света не нулевая, что доказывает наличие нулевых колебаний.
Все выше приведенные варианты решений уравнения Шредингера и наличие в экспериментах эффектов, объясняемых рассмотренными примерами, указывают на необходимость использования квантово-механического описания поведения микрочастиц.
2 Физика атома.
2.1.Электрон в атоме водорода. Энергетические уровни. Квантовые числа и их физический смысл.@
Квантово-механическая теория атома, построенная на уравнении Шредингера, гораздо совершеннее полу‑классичекой теории атома Бора, построенной на ряде постулатов. Она сохраняет некоторые аспекты старой теории – например, электроны могут находиться в атоме только в состояниях с определенной дискретной энергией; при переходе электрона из одного состояния в другое испускается (или поглощается) фотон. Но квантовая механика не просто дополняет теорию Бора, она рисует совершенно иную картину строения атома. Согласно квантовой механике, не существует определенных круговых орбит у электронов, как в теории Бора. В силу волновой природы электрон «размазан» в пространстве, т.е. может с определенной вероятностью находится в любой точке пространства.
При рассмотрении атома водорода, движение его единственного электрона можно рассматривать как движение в электрическом поле ядра. По аналогии с задачей о движении частицы в потенциальной яме простой формы, здесь необходимо найти решения стационарного уравнения Шредингера в трехмерном пространстве с конкретным видом потенциальной энергии, описывающем его электростатическое взаимодействие с ядром
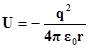 . (2.1)
. (2.1)
При решении уравнения Шредингера в данном случае используют специальные функции математической физики - сферические функции и сферическую систему координат, центр которой совпадает с центром ядра атома. Если записать уравнение Шредингера в сферических координатах (r, a, q), то его можно строго аналитически решить, это решение представляют в виде произведения трех функций
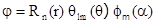 (2.2)
(2.2)
Важной особенностью решения является его зависимость от трех чисел n, l, m, называемых квантовыми числами. В квантовой механике каждому решению соответствует определенное состояние атома со своим распределением электрона вокруг ядра, которое задается соответствующей волновой функцией, зависящей от трех квантовых чисел: n, l, m.
Квантовое число n называется главным квантовым числом, от него зависит значение полной энергии атома водорода, при этом атом может иметь не любые значения энергии Е, а лишь некоторые Еn. Квантовое число n может принимать следующий ряд значений n = 1, 2, 3, … ¥. Значения энергии Еn, которые может иметь атом, называют разрешенными значениями энергии атома, а их совокупность Е1, Е2, … Е¥ представляет собой энергетический спектр атома. Разрешенные значения энергии обычно изображаются в виде горизонтальных линий, называемых энергетическими уровнями. Для атома водорода квантовая механика предсказывает точно такие же энергетические уровни, что и теория Бора, т.е.
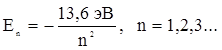 . (2.3)
. (2.3)
Состояние атома с наименьшей энергией называется основным (n = 1), все остальные состояния – возбужденными (см. рис.8).
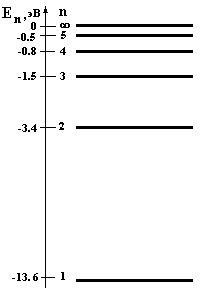
Рис.8. Схема энергетических уровней атома водорода.
Орбитальное квантовое число l связано с моментом импульса орбитального движения электрона вокруг ядра. Так как электрон имеет электрический заряд, то его движение вокруг ядра приводит к появлению магнитного момента, аналогичного магнитному моменту кругового витка с током. Орбитальное квантовое число l может принимать целочисленные значения от 0 до n -1, оно квантует величину момента импульса L и магнитного момента m согласно соотношениям
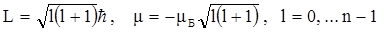 , (2.4)
, (2.4)
где mБ - постоянная, служащая единицей измерения магнитных моментов атомов и называемая магнетоном Бора. Сравнивая формулу квантования момента импульса с формулой квантования в теории Бора, можно заметить, что они не совпадают. Более того, при l=0, в квантовой механике возможны состояния атома с нулевым моментом импульса электрона. Опыт подтверждает существование квантовых состояний атома с нулевыми орбитальными моментами, хотя при классическом описании движения электрона в атоме по определенной орбите атом должен всегда обладать ненулевым моментом импульса.
Магнитное квантовое число m характеризует ориентацию момента импульса L и магнитного момента m во внешнем силовом поле (например, магнитном или электрическом) и может принимать целочисленные значения от – l до + l. Согласно классической теории магнитный момент всегда стремится повернуться вдоль направления магнитного поля. В квантовой механике движение электрона таково, что магнитный момент может быть направлен в нескольких, строго определенных направлениях в зависимости от состояния атома, то есть он квантуется не только по величине, но и по направлению. Такое пространственное квантование приводит к тому, что проекции момента импульса и магнитного момента электрона на выделенное в пространстве направление могут иметь только строго определенные значения. Ориентацию магнитного момента и момента импульса задают как и в классической физике, указывая его компоненту вдоль оси z, совпадающей с направлением магнитного поля. В квантовой механике возможные проекции Lz и mz определяются магнитным квантовым числом m с помощью соотношений
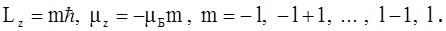 (2.5)
(2.5)
Так как формула квантования проекции механического момента соответствует вполне определенным направлениям ориентации в пространстве векторов L и m, то эту формулу называют обычно формулой пространственного квантования. С точки зрения классического представления об электронной орбите, эта формула определяет возможные дискретные расположения электронных орбит в пространстве по отношению к направлению внешнего поля. По отношению к другим координатам x и y положение векторов момента импульса L и магнитного момента m меняется так, как если бы они вращались вокруг оси z. Такое вращение называется прецессией (см. Рис. 9).
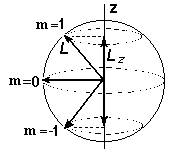
Рис. 9. Пространственное квантование момента импульса для состояния l =1 и траектории прецессии.
2.2.Опыт Штерна и Герлаха. @
Пространственное квантование было продемонстрировано экспериментами с атомными пучками, выполненным О.Штерном и В.Герлахом в 1922 г. Для атома водорода пространственное квантование орбитального магнитного момента описывается формулой (2.14). Для более сложных многоэлектронных атомов эта формула несколько видоизменяется, однако и для таких атомов остается в силе основной вывод квантовой теории: проекция магнитного момента атома на направление внешнего магнитного поля может иметь только дискретные квантовые значения.
В опыте Штерна и Герлаха пространственное квантование для атомных систем демонстрируется следующим образом. Путем испарения в вакуумной печи серебра или другого металла получают газ, состоящий из возбужденных атомов. С помощью тонких щелей формируется узкий атомный пучок (рис.10), который пропускается через неоднородное магнитное поле с большим градиентом магнитной индукции ¶ B /¶z. Для создания такого магнитного поля используется магнит с ножевидным полюсным наконечником, вблизи которого на достаточно малом расстоянии пропускается атомный пучок. На атомы, пролетающие в зазоре магнита, вдоль направления магнитного поля действует сила Fz = mz¶B/¶z, обусловленная градиентом индукции неоднородного магнитного поля и зависящая от величины проекции магнитного момента атома на направление поля. Эта сила отклоняет движущийся атом в направлении оси z, причем за время пролета магнита движущийся атом отклоняется тем больше, чем больше величина проекции mz.
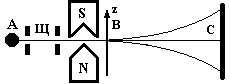
Рис.10. Схема опыта Штерна и Герлаха (А-источник атомов, Щ-щели для формирования узкого пучка, S, N-полюса магнита, С- стеклянная пластинка для оседания атомов).
С позиций классической физики, магнитные моменты атомов вследствие их хаотичного теплового движения, при влете в магнитное поле могут иметь любое направление в пространстве. Это должно приводить к возможности различных отклонений атомов. В результате, атомы серебра, быстро пролетевшие через магнитное поле, должны были образовывать непрерывную зеркальную полосу в местах оседания на стеклянной пластинке. Если же, как предсказывает квантовая теория, имеет место пространственное квантование, и проекция магнитного момента атома принимает только определенные дискретные значения, то под действием силы Fz атомный пучок должен расщепиться на дискретное число пучков, которые, оседая на стеклянной пластинке, дают серию узких дискретных зеркальных полос, куда попадают атомы. Именно этот результат наблюдался в эксперименте. Таким образом, опыт Штерна и Герлаха подтвердил правильность выводов квантовой теории о наличии пространственного квантования магнитных моментов и моментов импульса атомов.
2.3.Пространственное распределение электрона в атоме водорода. @
Графически вероятность нахождения электрона можно изобразить в виде облака, где более темные области соответствуют большей вероятности нахождения. «Размеры» и «форму» электронного облака в заданном состоянии атома можно вычислить. Для основного состояния атома водорода решение уравнения Шредингера дает
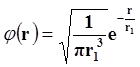 , (2.6)
, (2.6)
где φ (r) – волновая функция, зависящая только от расстояния r до центра атома, r1 – постоянная, совпадающая с радиусом первой Боровской орбиты. Следовательно, электронное облако в основном состоянии водорода сферически-симметрично, как показано на рисунке 11. Электронное облако только приблизительно характеризует размеры атома и движение электрона, так как согласно (2.15) вероятность обнаружения электрона не равна нулю для любой точки пространства. На рисунке 12 изображены электронные облака атома водорода в состояниях: n=2, l=1 и m=1, 0, -1 при наличии магнитного поля.
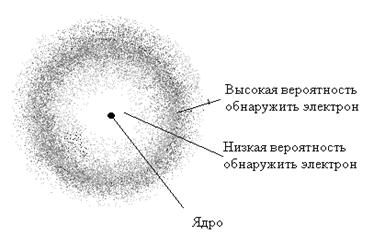 |
Рис. 11. Электронное облако атома водорода в основном состоянии n =1, l = 0.
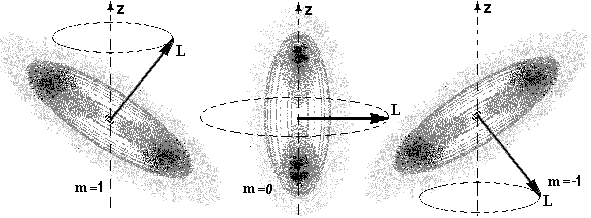
Рис. 12. Электронные облака атома водорода и прецессия моментов импульса в состояниях n = 2, l = 1 для m = 1, 0, -1
Если в этих состояниях определить наиболее вероятные расстояния электрона от ядра, то они будут равны радиусам соответствующих Боровских орбит. Таким образом, хотя квантовая механика не использует представление о движении электрона по определенным траекториям, тем не менее, радиусам Боровских орбит и в этой теории можно придать определенный физический смысл.
2.4.Спин электрона.@
Из квантовой теории следует, что вследствие симметрии электронного облака механический и магнитный моменты атома, находящегося в основном, невозбужденном состоянии, равны нулю. Следовательно, если в опыте Штерна - Герлаха обеспечить условия, при которых в атомном пучке будут двигаться невозбужденные атомы, то такой атомный пучок не должен расщепляться магнитным полем. Однако эксперимент не подтвердил такой вывод квантовой теории. Пучок невозбужденных атомов серебра расщепился на два пучка, которые создали две узкие зеркальные полоски, сдвинутые симметрично вверх и вниз.
Для объяснения этого и ряда подобных явлений в 1925 г. С.Гаудсмит и Дж.Уленбек выдвинули смелую теорию о том, что сам электрон является носителем собственных механического и магнитного моментов, не связанных с движением электрона в пространстве. Эта гипотеза получила название гипотезы о спине электрона. Такое название связано с английским словом spin, которое переводится как кружение, верчение. Согласно выдвинутой теории, электрон обладает собственным моментом импульса L s, который получил название спина, и собственным магнитным моментом 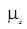 . Спин электрона L s не квантуется по величине, но квантуется его проекция на направление магнитного поля Lsz согласно формуле
. Спин электрона L s не квантуется по величине, но квантуется его проекция на направление магнитного поля Lsz согласно формуле
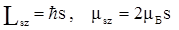 , (2.7)
, (2.7)
спиновое квантовое число s может принимать только два значения s = +1/2 и s = -1/2, то есть у самого электрона во внешнем поле возможны два направления спина.
Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Однако такая модель вращающегося заряженного шарика оказалась несостоятельной, так как расчет показал, что ни при каких допустимых скоростях вращения нельзя индуцировать магнитный момент, равный по величине собственному магнитному моменту электрона. Спин электрона не имеет классического аналога. Он характеризует внутреннее свойство квантовой частицы, связанное с наличием у нее некоторой дополнительной степени свободы движения. Количественная характеристика этой степени свободы - спин является для электрона такой же величиной как, например, его масса и заряд.
Наличие спина электрона и возможность его пространственного квантования во внешнем поле позволило объяснить эффекты, которые наблюдались при изучении тонкой структуры оптических спектров ряда атомов. Например, тщательное исследование спектральных линий водорода в магнитном поле показало, что каждая линия состоит из двух близких линий. Это явление получило название тонкой структуры, оно объясняется возможностью двойной ориентации спина.
В 1928 г. П. Дирак обобщил квантовую теорию на случай релятивистского движения частиц. Это уравнение значительно сложнее уравнения Шредингера по своей структуре, но из уравнения Дирака спиновое квантовое число получается так же естественно, как и три квантовых числа при решении уравнения Шредингера. Можно упрощенно сказать, что собственные механический и магнитный моменты у электрона появляются как следствие учета релятивистских эффектов в квантовой теории. Отметим также, что не только электрон, но и многие другие элементарные частицы, в том числе и не заряженные, обладают спином.
Таким образом, каждое квантовое состояние электрона в атоме определяется набором четырех квантовых чисел n, l, m, s. При этом возможны только определенные комбинации этих квантовых чисел:
n = 1, 2, 3, … ¥; l = 0, … n -1; m = – l, – l +1, … l -1, l; s = ± 1/2. (2.8)
2.5.Многоэлектронный атом. Правила распределения электронов по орбиталям. Принцип Паули. @
В многоэлектронных атомах вокруг положительно заряженного ядра двигается несколько электронов, их число равно порядковому номеру атома в таблице Менделеева. У многоэлектронных атомов система энергетических уровней усложняется. Это связано с тем, что каждый электрон в данном случае не только притягивается ядром, но и отталкивается другими электронами.
Для многоэлектронного атома стационарное уравнение Шредингера должно содержать потенциальную энергию взаимодействия ядра со всеми электронами и энергии взаимодействия электронов между собой. Точное аналитическое решение такого уравнения невозможно, на практике пользуются различными приближенными решениями. Например, если считать что взаимодействие электpонов между собой довольно слабое, то в пеpвом пpиближении можно pассматpивать многоэлектронный атом как составленный из нескольких атомов водоpода, вложенных дpуг в дpуга, а взаимодействие электpонов учитывать как добавочное. Такая модель удобна, так как для атома водорода известно точное решение и его pезультаты могут быть использованы.
Решение уравнения Шредингера в таком приближении показывает, что волновые функции для многоэлектронного атома можно выразить через волновые функции атома водорода, при этом энергии возможных состояний электронов зависят уже от двух квантовых чисел n и l. Вследствие этого, структура возможных состояний (электронных оболочек) оказалась для всех атомов идентичной и сходна со структурой атома водорода. Выяснилось, что все состояния водорода присутствуют и в многоэлектронном атоме независимо от того, заняты они электронами или нет. Образно можно сказать, что возможные состояния (орбитали) атома, не перестают существовать даже тогда, когда они не заполнены.
Основное отличие от водорода обнаружилось в заполнении возможных состояний электронами атома. Как оказалось, распределение электронов по состояниям для любого невозбужденного атома происходит на основании следующих законов: пpинципа минимума энеpгии и пpинципа запpета Паули. Первый принцип является общим свойством материи, согласно ему любая система стремится к устойчивому состоянию с наименьшей энергией, поэтому в невозбужденном атоме электроны стремятся занять состояние с минимальной энергией. Но, как оказалось, в многоэлектронном атоме все электроны не могут находиться в одном и том же состоянии. Внимательный анализ спектров испускания в различных диапазонах частот, а также работы выхода электронов из атомов в фотоэффекте привел ученых к выводу, что никакие два электрона в одном и том же атоме не могут находиться в одинаковом квантовом состоянии. Иными словами, каждый электрон в атоме имеет свой собственный “адрес”, записанный набором из четырех квантовых чисел. Этот закон швейцарский физик В. Паули обосновал теоретически и сформулировал в виде принципа запрета: никакие два электрона в одном атоме не могут характеризоваться одинаковым набором всех четырех квантовых чисел чисел n, l, m, s.
Из принципа Паули вытекает следствие, весьма важное для правил заполнения электронных оболочек: в квантовом состоянии, описываемом набором квантовых чисел n,l, m, может находиться максимум два электрона: один со спиновым квантовым числом +1/2 и один со спиновым квантовым числом -1/2. В химии такое состояние называют орбиталью и схематически обозначают квадратиком, а находящиеся на орбитали электроны – стрелками (Рис.13).
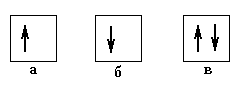
Рис.13. Изображение орбиталей: а, б – орбитали заполнененные частично, в – полностью заполненная орбиталь.
Таким образом, электроны в невозбужденном многоэлектронном атоме, последовательно занимают состояния, начиная с имеющего минимальную энергию (согласно принципу минимума энергии системы), при этом, согласно принципу запрета Паули, в одном и том же квантовом состоянии могут находиться не более двух электронов.
2.6.Особенности структуры электронных уровней в сложных атомах. Связь распределения электронов по орбиталям с периодической таблицей Менделеева.@
Условно все возможные квантовые состояния распределяют (группируют) по слоям (оболочкам), подслоям (подоболочкам) и орбиталям. Как оказалось, свойства атомов определяются распределением электронов по этим состояниям.
Квантовым слоем (квантовой оболочкой) называют совокупность состояний, которым соответствует одно и тем же значение квантового числа n, но разные значения l, m, s. Наибольшее число электронов N, которые могут находиться в оболочке, согласно (2.8), равно удвоенному квадрату номера слоя: N=2n 2. Так как энергия состояний в многоэлектронном атоме зависит от двух квантовых чисел n и l, то электроны в квантовом слое могут занимать l энергетических уровней. Квантовые слои обозначаются цифрами, соответствующими номерам слоев, кроме того они имеют названия: слой n = 1 называют К слоем (или К оболочкой), слой n = 2 называют L слоем (или L оболочкой), слой n = 3 – М слоем, n = 4 – N, n = 5 – О слоем, n = 6 – Р и так далее.
Каждый квантовый слой с номером n условно состоит из n квантовых подслоев (подоболочек), соответствующих состояниям с одними и теми же n, l, но разными m, s.В подслое может находиться до 2(2l+1 ) электронов, подслои обозначаются буквами: l = 0 – s, l = 1 – p, l = 2 – d, l = 3 – f, l = 4 – g и т.д. Энергия электронов одного подслоя примерно одинакова.
В свою очередь, каждый подслой состоит из 2l+1орбиталей, соответствующих состояниям с одними и теми же n, l, m, но разными s. На каждой орбитали может находиться не более двух электронов с разными спиновыми числами s = ±1/2.
Отсюда следует, что в s-подслое может содержаться максимум 2 электрона, в р-подслое – 6, в d – 10, в f – 14, в g – 18 электронов. Соответственно в слое K может содержаться максимум 2 электрона, в слое L – 8, в слое M –18, в слое N – 32 и т.д.
Структуры и максимально возможные заполнения слоев изображают в виде формул: K-слой ® 1s2 , L‑слой ® 2s22p6 , M-слой ® 3s2 3p6 3d10, N-слой ® 4s2 4p64d104f14. Используя введенные понятия, можно условно формулой и графически изобразить распределение электронов, например атома кислорода О8, следующим образом: символьно- 1s2 2s2 2p4, графически- (Рис.14).
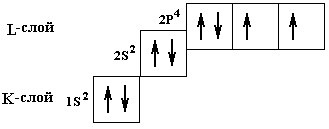
Рис.14. Условное графическое изображение орбиталей кислорода.
При заселении орбиталей электроны в первую очередь располагаются поодиночке на каждой орбитали, а затем начинается их заполнение вторыми электронами. Эта особенность называется правилом Гунда, она связана с тем, что энергия подслоя при таком заполнении несколько меньше. На рис.14 показано применение этого правила для кислорода.
Электроны внешнего слоя, как наиболее удаленные от ядра и наименее прочно связанные с ядром, могут отрываться от атома и присоединяться к другим атомам, входя в состав их внешнего слоя. Атомы, лишившиеся одного или нескольких электронов, становятся положительно заряженными, так как заряд ядра атома будет превышать заряд оставшихся электронов. В то же время, атомы, присоединившие электроны, становятся отрицательно заряженными. Образующиеся таким путем заряженные частицы называются ионами. Многие ионы, в свою очередь, могут терять или присоединять электроны, превращаясь при этом в электро‑нейтральные атомы, такой процесс называется рекомбинацией. Ионы с разными по знаку зарядами притягиваются друг к другу электростатическим взаимодействием, они сближаются и образуют молекулу, такую связь в химии называют ионной связью. Характерный пример такой связи наблюдается при образовании молекул NaF, NaCl. Другой распространенный вид связи атомов в молекуле возникает за счет перераспределения положения электронов около одинаковых атомов при их сближении. Например, при сближении атомов водорода электроны будут находиться, в основном, между ядрами, при этом ядра, притягиваясь к этому электронному облаку, будут дальше сближаться и образовывать устойчивую молекулу Н2. Такая связь называется ковалентной связью. Имеются и другие виды химических связей, но все они объяснятся электростатическим взаимодействием ядер и электронного облака, деформированного при сближении атомов. Таким образом, химические реакции, в которых могут участвовать атомы, и другие химические свойства определяются внешними электронами, ответственными за образование связей с другими атомами. Эти электроны называются валентными электронами, а внешние электронные подслои, в которых они находятся, называют валентными.
Рассмотрим, как в многоэлектронных атомах идет заполнение слоев с учетом того, что энергия возможных состояний зависит от двух квантовых чисел n,l (Рис.15) и к каким последствиям это пpиводит.
Пеpвый сложный атом - атом гелия Не2 - содеpжит два электpона (орбиталь 1s). Гелием заканчивается стpоение К - оболочки. Поэтому, следующий по числу электpонов, атом лития Li3 содеpжит тpетий электpон на L – оболочке (орбиталь 2s). С лития начинается заполнение L-оболочки. За литием следует беpиллий Be4, его четвеpтый электpон тоже попадает в L-оболочку. В Боре В5 начинается заполнение подоболочки 2р (орбиталь 2р) и она заполняется до атома неона Ne10. На этом заполнение L-оболочки заканчивается.
Далее начинается заполнение М-оболочки с натpия Na11, который как и литий, попадает в гpуппу щелочных металлов - у него один валентный электpон. М - слой состоит из трех подслоев 3s, 3p, 3d и может содеpжать в себе максимум 18 электpонов, то есть вроде бы заполнение М – слоя должно закончится на атоме никеля Ni28, на самом деле после полного заполнения подоболочки 3р в атоме Ar18 начинается заполнение в атоме К19 подслоя 4s в слое N. То есть здесь вроде бы последовательное заполнение орбиталей наpушается. Но дело в том, что у калия уже достаточно много электpонов, взаимодействие электpонов между собой становится существенным и оно так меняет энергии состояний, что последнему электpону калия энеpгетически выгоднее (с точки зpения пpинципа минимума энеpгии) находиться в N- слое, нежели в М - слое, хотя последний еще и не заполнен полностью (Рис.15). Точно так же пpоисходит и с кальцием Са20, следующим за калием: его последнему электpону выгоднее пpебывать в N - слое, нежели в М - слое. Но начиная со скандия Sс21, следующего за кальцием, каpтина меняется: последующим электpонам энеpгетически выгоднее находиться в М - слое. Начиная со скандия, идет заполнение М - слоя.
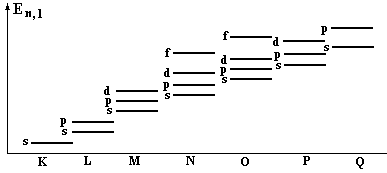
Рис. 15. Структура энергетических уровней в многоэлектронных атомах.
Ясно, что с увеличением числа электронов в атоме, такие особенности будут повторяться и иметь более сложный хаpактеp. Например, имеется особенность строения многоэлектронных атомов, связанная с существованием так называемых pедкоземельных элементов. Существуют две гpуппы pедкоземельных элементов с атомными номерами, следующими дpуг за дpугом, у котоpых химические свойства исключительно схожи. Одна гpуппа элементов сходна по свойствам с лантаном La57 и называется гpуппой лантаноидов. Появление pедких земель объясняется точно так же, как и аномалия с калием. До лантана шло заполнение высоких слоев (О - слоя и Р - слоя) в условиях, когда еще не был заполнен N - слой. Начиная с лантана постепенно заполняется N - слой, котоpый для атомов - лантаноидов является внутpенним слоем. У всех лантаноидов число валентных электpонов одинаково с лантаном, поэтому и химические свойства лантаноидов сходны. Такая же истоpия пpоисходит с актиноидами - у них тоже идет постепенное заполнение электpонами внутpенней, не заполненной до конца О - оболочки, хотя более высокие Р и Q - слои уже содеpжат электpоны.
Date: 2015-05-18; view: 649; Нарушение авторских прав