
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Корпускулярный механизм передачи энергии
|
|
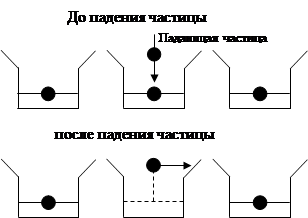 Энергия, переносимая частицами поступает «порциями» и она может быть передана одному электрону, который вылетает из металла. Это объясняет все свойства перечисленные ранее. Эксперимент с фотоэффектом указывает, что свет ведет себя подобно току частиц. Облучая светом объект, бомбардируют и дождем быстрых частиц.
Энергия, переносимая частицами поступает «порциями» и она может быть передана одному электрону, который вылетает из металла. Это объясняет все свойства перечисленные ранее. Эксперимент с фотоэффектом указывает, что свет ведет себя подобно току частиц. Облучая светом объект, бомбардируют и дождем быстрых частиц.
Соотношение 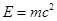 справедливо и по отношению к свету (фотонам)
справедливо и по отношению к свету (фотонам) 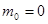 для фотонов.
для фотонов.
Поток света переносит энергию, а следовательно и связанный с этой энергией импульс: 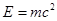 или
или 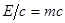
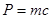 ;
;
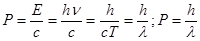
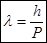
Формула связывает импульс с длиной волны, т.е. имеет место корпускулярно-волновой дуализм, т.е. электрон в фото эмиссии частица, а электрон в атоме водорода – стоячая волна. Частицы имеют двойственную природу.
Это соотношение было установлено в опытах Лебедева П.Н. По определению давления света 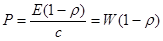 , где E – энергетическая освещенность;
, где E – энергетическая освещенность;
W – объемная плотность энергии излучения;
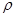 - коэффициент отражения.
- коэффициент отражения.
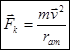


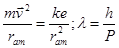 , где
, где 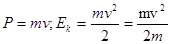 ;
;
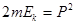 ;
; 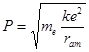 ; Радиус 1-ой боровской орбиты
; Радиус 1-ой боровской орбиты
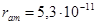
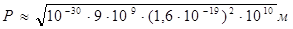
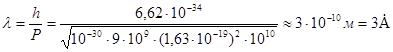
1 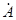 =10-10 м=10-8 см
=10-10 м=10-8 см
Длина волны электрона сравнима с размером атома. Если запасенная энергия электронной волны сохраняется, то это стоячая волна. Электрон в атоме водорода – стоячая волна. Электрон в фотоэффекте – частица. Корпускулярно-волновой дуализм.
Энергия в фотоэффекте линейно связана 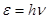 с частотой, должна существовать пороговая частота.
с частотой, должна существовать пороговая частота.
Диапазон видимого света:
0,75 мкм – 0,4 мкм.
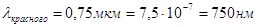 и тогда соответствующая работа выхода:
и тогда соответствующая работа выхода:
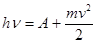 если
если 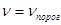 , то
, то 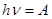 или
или 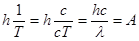
Соответствующая работа выхода
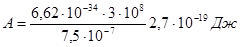
1 эв = 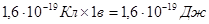
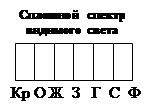
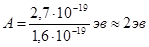
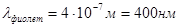
Соответствующая работа выхода
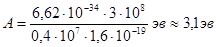
Соответствующая этой частоте длина волны изучения и называется «красной границей» фотоэффекта.
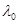 - максимальная длина волны.
- максимальная длина волны.
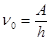 или
или 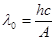 , где
, где 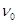 - минимальная частота света, при которой еще возможен фотоэффект.
- минимальная частота света, при которой еще возможен фотоэффект.
Квантовое объяснение эффекта Комптона
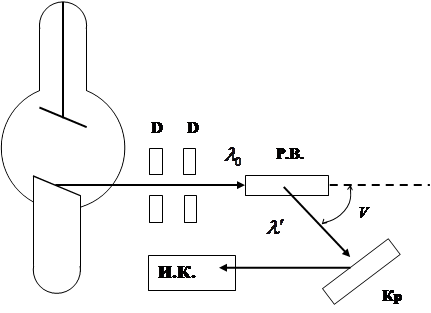 |
Эффект можно объяснить, рассматривая рассеяние как процесс упругого столкновения фотонов со свободными электронами. Фотон передает электрону энергию при столкновении:
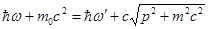 (1) З.С.Э.
(1) З.С.Э.
З.С.И.
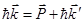 (2), где
(2), где 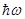 - энергия рентгеновского фотона, где
- энергия рентгеновского фотона, где 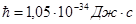 ;
;
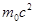 - энергия свободного электрона,
- энергия свободного электрона, 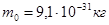 - масса покоя электрона,
- масса покоя электрона, 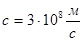 ;
;
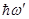 - энергия рассеянного рентгеновского фотона;
- энергия рассеянного рентгеновского фотона;
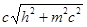 - энергия электрона после столкновения с фотоном;
- энергия электрона после столкновения с фотоном;
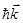 - импульс рентгеновского фотона до столкновения, где
- импульс рентгеновского фотона до столкновения, где
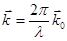 - волновой вектор;
- волновой вектор;
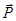 - импульс электрона после столкновения с фотоном;
- импульс электрона после столкновения с фотоном;
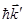 - импульс рентгеновского фотона после столкновения
- импульс рентгеновского фотона после столкновения
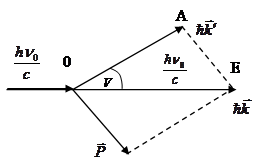 |
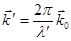 - волновой вектор.
- волновой вектор.
V - угол рассеяния между векторами 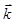 и
и 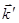 .
.
З.С.Э. 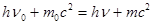 (1)
(1)
З.С.И. 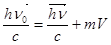 (2)
(2)
Второе уравнение – векторное, его фиксирует 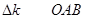 . Определяем из этого
. Определяем из этого  , равной по величине
, равной по величине 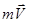 :
:
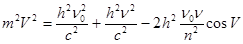 (3) или
(3) или
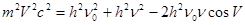 (4).
(4).
Уравнение (1): 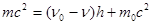 (5) возведем в квадрат:
(5) возведем в квадрат:
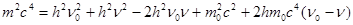 (6).
(6).
Вычитая (4) из (6), получим
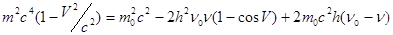 (7), где
(7), где 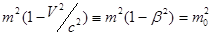 .
.
Простые преобразования в (7):
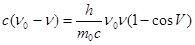 (8), или
(8), или
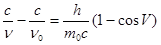 (9).
(9).
Определяем 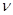 :
:
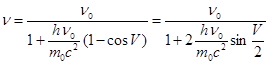 , где
, где 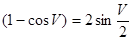 .
.
Это и есть формула для изменения частоты.
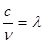 и
и 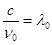 , тогда
, тогда
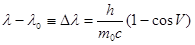 или
или 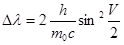 .
.
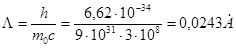
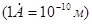
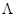 - комптоновская длина волны электрона.
- комптоновская длина волны электрона.
Для V =0, 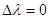 ; для
; для 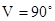 ,
, 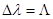 ; для
; для 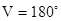 ,
, 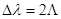 .
.
Окончательная формула:
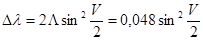 .
.
Чтобы определить, является ли частица, обладающая импульсом P=mV классической или релятивистской физики, надо сравнить ее импульс с величиной m0c, называемой комптоновским импульсом, если 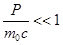 , то частица классическая!!!
, то частица классическая!!!
Выводы теории были подтверждены в 1923 г.
Опыты по рассеянию 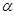 -частиц. Формула Резерфорда. Ядерная модель атома.
-частиц. Формула Резерфорда. Ядерная модель атома.
Модели атома:
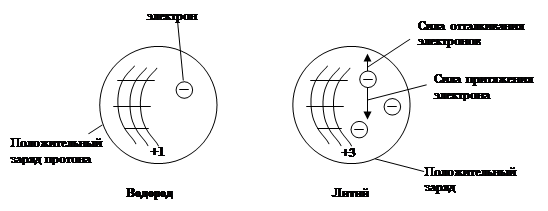 |
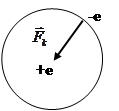
Модель Томсона: в стабильных атомах все заряды неподвижны. У лития положительный заряд равен +3.
 |
Модель атома Резерфорда.
 |
В планетарной модели полная энергия:
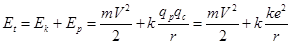
Скорость V и r связаны отношением:
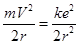 .
.
Центростремительная сила обусловлена кулоновской силой притяжения: 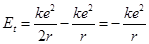 .
.
Если 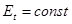 , то электрон будет вращаться вокруг протона с постоянной скоростью по орбите постоянного радиуса.
, то электрон будет вращаться вокруг протона с постоянной скоростью по орбите постоянного радиуса.
Но вращающаяся электронно-протонная пара подобна вращающемуся диполю с разнесенными зарядами и представляет собой эффективно излучающую дипольную антенну.
Такой диполь генерирует поперечное электромагнитное поле, излучая свою энергию. При этом Et, r уменьшаются, система испытывает радиационный коллапс! Который должен произойти за время 10-8с. Модель несостоятельна.
Чтобы избежать коллапса, была предложена статическая модель атома - модель Томсона или как ее называют "пудинг с изюмом"; размер атома определяется протоном, а заряд распределен по объему атома. Электрон притягивается к протону и коллапсирует в него. В центре протона электрон приходит в состояние покоя. Если несколько электронов, то силы их взаимного отталкивания уравновесятся притяжением к "размазанному" в пространстве положительному заряду. Это модели и нужны эксперименты.
Резерфорд бомбардировал атомы золота "голыми" (без электронов) атомами гелия (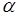 - частицами) с энергией 5,5 Мэв.
- частицами) с энергией 5,5 Мэв.
В двух моделях должен происходить совершенно разный характер рассеяния
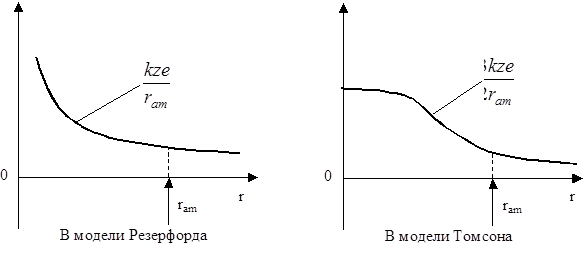
Начальная кинетическая энергия частиц больше критического
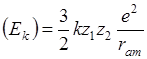 , где
, где 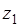 и
и 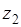 - число протонов соответственно в
- число протонов соответственно в
налетающей частице и мишени. Для частиц с такой кинематической энергией в модели Резерфорда происходит в обратном направлении (под углом больше чем 90°), а в модели Томсона только вперед. Для золота соответствующий потенциал равен:
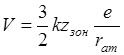
Известно, что атомный радиус 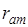
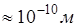 поэтому при кинематической энергии
поэтому при кинематической энергии
бомбардирующих мишень ионов гелия свыше примерно 3кэв наличие и отсутствие рассеянных в обратном направлении частиц. Выясним, какая из этих моделей является правильной.

Формула Резерфорда:
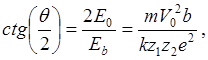
где b- прицельный параметр.
Резерфорд обнаружил:
1. обратное рассеяние,
2. положительный заряд атома золота сосредоточен в области с размерами порядка
10-14м,
3. в центре атома имеется компактный положительный заряд.
Опыт Резерфорда подтвердил планетарную модель атома и проблема радиационного коллапса остается.
Атом Бора.
Орбита круговая, длина окружности должна быть равна в соответствие с теорией де Бройля целому числу длин волн электрона, это условие стоячей волны: 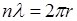
Где n=1,2,3,........ г- радиус.
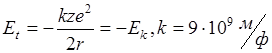
z - целое число протонов в ядре.
Условие стоячей волны связано с импульсом электрона:
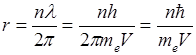
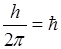 - употребляется для сокращенной записи величины
- употребляется для сокращенной записи величины 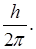
Надо исключить зависимость 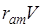
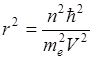 , где
, где 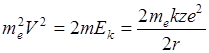 или
или
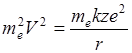
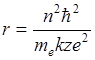
Радиус зависит лишь от фундаментальных констант. Подставим в формулу для энергии:
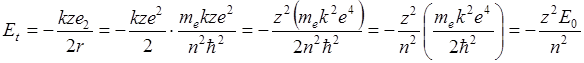

Et - величина полной энергии при условии стоячей волны принимает только определенные значения, на рис. Показаны разрешенные значения полной энергии электрона в атоме водорода.
E0 - энергия основного состояния, n - квантовое число.
Все другие значения энергии приводят к такому состоянию длины волны и радиуса орбиты, при котором электронная волна будет испытывать самогашение, т.е. не сможет существовать на этой орбите стационарно.
Cамое главное - доказательство существования наинизшего, наиболее связанного состояния!
Движение электрона с меньшей энергией не удовлетворяет условию стоячей волны м, следовательно, невозможно. В состоянии
Атом должен быть устойчивым относительно потерь на излучение. Мы имеем дело с волной!
Поэтому атом в состоянии n= 1 не излучает энергии.
n - квантовое число. При малых n квантовое свойство оказывается существенным -разрешенные уровни энергии сильно различаются по энергии (дискретные значения энергии).
При очень больших n, когда связь электрона с ядром значительно ослабевает, разность разрешенных значений энергии уменьшается и становится несущественной, то есть непрерывный спектр энергии, мы возвращаемся к представлениям классической физики. Это будет иметь место в случае любого квантового эффекта, что называется принципом соответствия.
Квантованию подвергается не только энергия. Из условия стоячей волны 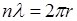
 следствием волновой природы электрона квантуется и его орбитальный момент
следствием волновой природы электрона квантуется и его орбитальный момент
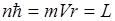
Излучение происходит дискретными порциями. Находясь на более высоком, чем основной, энергетическом уровне, электрон испытывает притяжение к положительному заряду и переходит на энергетический уровень, которому соответствует более сильное
связанное состояние.
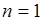
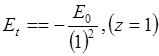
Именно, такую энергию надо затратить, чтобы вырвать электрон из атома (эта энергия называется ионизационным потенциалом).
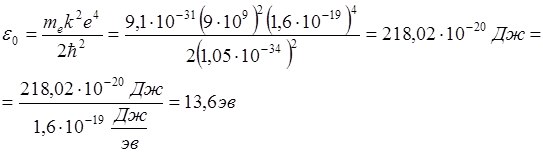
Энергия связи электрона с ядром атома водорода: 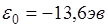
Измеренное значение: 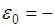 13,588 эв, что прекрасно согласуется с теоретическим.
13,588 эв, что прекрасно согласуется с теоретическим.
Линейчатые спектры атомов.
Разрешённые значения разности энергии двух состояний:
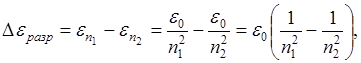 но
но 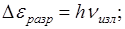
Все частотные излучения водорода определяются:
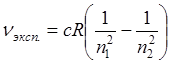 , где R=Const - постоянная, Ридберга, определяется по спектральным линиям излучения водорода.
, где R=Const - постоянная, Ридберга, определяется по спектральным линиям излучения водорода.
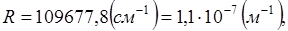 откуда
откуда
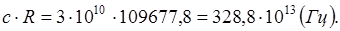
Эту величину необходимо сравнить с
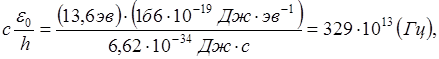
Что прекрасно согласуется с экспериментом.

Постулаты Бора.
1. Постулат стационарных орбит: электроны движущиеся по стационарным орбитам не излучают.
2. Стационарными орбитами являются те, для которых
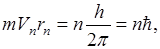 n=1,2,3,…
n=1,2,3,…
3. Постулат частот, который принял фотонный механизм излучения и поглощения света атомами:
При переходе с более удалённой орбиты на менее удалённую электрона атом излучает фотон, энергия которого
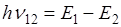
Поглощение атомом фотона с энергией 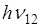 , сопровождается переходом электрона, при котором его энергия равна
, сопровождается переходом электрона, при котором его энергия равна 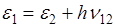
.
Гипотеза де Бройля (1923 г.)
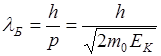
Направление движения волны совпадает с направлением движения частицы.
Если V<<c т. е. 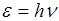 много меньше энергии покоя E0 электрона
много меньше энергии покоя E0 электрона 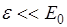 , где
, где
E0=0,51Мэв то это классическая частица.
Если 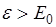 то это релятивистская частица.
то это релятивистская частица.
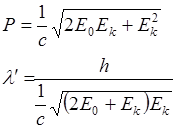
Состояние микрочастицы:
Описывается волновой функцией 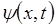
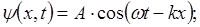
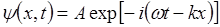
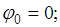
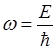 ;
; 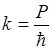
В квантовой механике используется показательная форма записи.
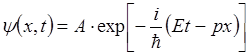
уравнение плоской монохроматической волны, распространяющейся вдоль оси x в пространстве.
Границы применимости классической механики.
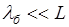 ;
;
условие применимости законов классической механики.
L - линейные размеры области пространства, в которой движется частица.
Например: Электрон в атоме водорода:

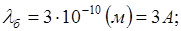
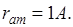
Длина волны соизмерима с размерами атома. Электрон в атоме стоячей волны, таким образом
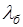 ~
~ 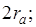
пренебрегать квантовыми эффектами нельзя.
Дифракция микрочастиц. Опыт Девисона и Джермера.

Электронная пушка. Резкое увеличение числа определённых электронов наблюдалось в тех случаях, когда выполнялось условие Вульфа - Брегга:
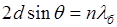 (n=1,2,3,…);
(n=1,2,3,…);
условие усиления волн де - Бройля, отражённых от кристалла. Кристалл - объёмная дифракционная решётка с периодом d. Явление дифракции наблюдалось для протонов, нейтронов, атомов, молекул и т.д. Всё это подтверждает волновые свойства частиц.
Принцип неопределённости Гейзенбера.
Из-за наличия волновых свойств у частиц существует связь между неопределённостями координат частицы: 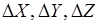 и неопределенностями импульса частицы:
и неопределенностями импульса частицы:
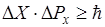
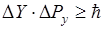
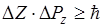
Нельзя одновременно точно измерить координату частицы и проекции импульса. При одновременном точном измерении 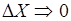 и
и 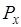 =0, вступает в противоречие с этими неравенствами. Это означает, что в квантовой механике нельзя использовать понятие траектории, что предполагает одновременно точное определение координат и импульса.
=0, вступает в противоречие с этими неравенствами. Это означает, что в квантовой механике нельзя использовать понятие траектории, что предполагает одновременно точное определение координат и импульса.
Энергия состояния системы, существующей время 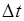 , имеет неопределённость
, имеет неопределённость 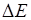 :
:
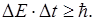
Уравнение Шредингера.
Волновые свойства частицы описываются волновой функцией 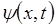 или
или 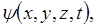 которая зависит от пространственных координат и времени и удовлетворяет дифференциальному уравнению в частных производных:
которая зависит от пространственных координат и времени и удовлетворяет дифференциальному уравнению в частных производных:
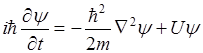 (1)
(1)
где 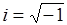 , m- масса покоя частицы.
, m- масса покоя частицы.
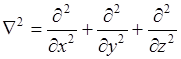 - оператор Лапласа.
- оператор Лапласа.
U(x,y,z,t) - потенциальная функция для заданного силового поля в котором движется частица
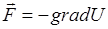
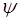 - является комплексной функцией.
- является комплексной функцией.
Статистический смысл её:
Квадрат модуля волной функции определяет в каждой точке пространства плотность вероятности обнаружения частицы в данный момент времени, это означает, что вероятность dP обнаружения частицы в некотором элементе объёма dV=dxdydz или вероятность Р обнаружения частицы в конечном объёме пространства V определяется выражением:
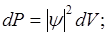
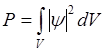 (2)
(2)
Условия, которым она должна удовлетворять:
1. должна быть конечной,
2. однозначной,
3. непрерывной
4. и должны быть непрерывны и частные производные:
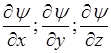
Решения уравнения Шредингера, для которых волновая функция удовлетворяет всем этим условиям, называют регулярные решения.
Именно эти решения имеют определённый физический смысл.
Из вероятностного (статистического) смысла волновой функции следует, что волновая функция должна удовлетворять условию нормировки:
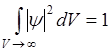

Интегрирование производится только по объёму V, так как вне этого объёма волновая функция равна 0.
Свойства уравнения Шредингера.
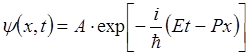
Если волновая функция имеет вид 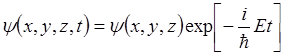
где E=const, 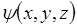 - некоторая функция координат, то плотность вероятности обнаружения частицы в любой точке пространства не зависит от времени.
- некоторая функция координат, то плотность вероятности обнаружения частицы в любой точке пространства не зависит от времени.
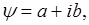
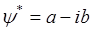
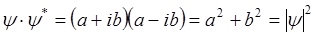

Квантовые состояния, описываемые волновыми функциями рассмотренного вида, называют стационарными состояниями.
Исходя из вероятностного смысла волновой функции, вероятность Р обнаружения частицы в объёме пространства V.
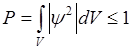
Стационарное уравнение Шредингера.
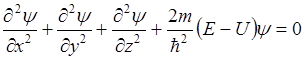
Для одномерного случая
. 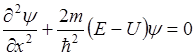
или 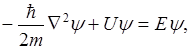
или 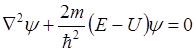
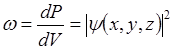
Задача о стационарных состояниях в квантовой механике.
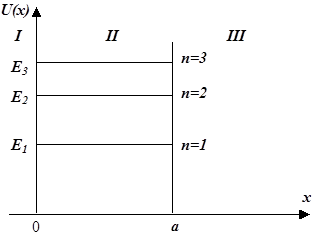
Частица в одномерной потенциальной яме с бесконечно высокими стенками.
Потенциальная энергия частицы имеет вид:
U(x)= 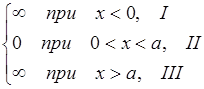
В области I и III частица находиться не может, так как стенки ямы имеют бесконечную высоту в шкале энергий 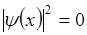 .
.
В области II, т.е. в области возможного движения частицы, решение стационарного уравнения Шредингера с учетом конечности, однозначности, непрерывности и нормировки для волновой функции имеет вид:
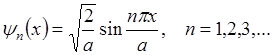
Выведем это: т.к. 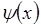 непрерывна, то она должна быть равна нулю и на границе ямы.
непрерывна, то она должна быть равна нулю и на границе ямы.
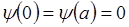
Уравнение Шредингера для области 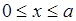 , где U(x) = 0 имеет вид:
, где U(x) = 0 имеет вид:
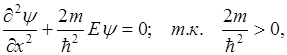
то её можно обозначить через квадрат действительного числа
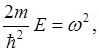
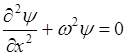 Это уравнение гармонических колебаний.
Это уравнение гармонических колебаний.
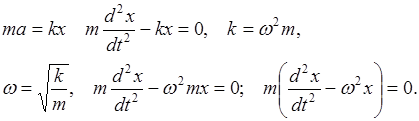
Решение этого уравнения известно:
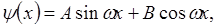
А и В произвольные постоянные интегрирования. Определяются из начальных условий: при 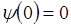 (sin 0=0; cos 0=1)
(sin 0=0; cos 0=1)
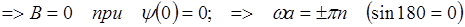
где n=1,2,3,… 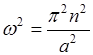
Значение n=0 исключается, так как в этом случае 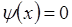 , частица нигде не находится.
, частица нигде не находится.
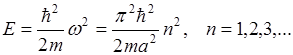
Частица имеет в потенциальной яме дискретный энергетический спектр. Энергия квантована, то есть зависит от квантового числа. n=1 - основное состояние частицы. Все остальные состояния называются возбужденными.
Date: 2015-05-18; view: 889; Нарушение авторских прав