
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные положения квантовой механики. 1 page
|
|
1.1.Противоречия классической физики: особенности строения атома, линейчатые спектры атомов, дифракция электронов, дифракция нейтронов.@
Корпускулярно-волновой дуализм свойств, обнаруженный у электромагнитного излучения, вскоре был обнаружен и у микрочастиц (молекул, атомов, ядер атомов, электронов, протонов, нейтронов и др.). В начале ХХ века в ряде экспериментов с микрочастицами, были обнаружены явления, которые не могли быть объяснены классической механикой, созданной для макротел.
Первая серия таких явлений связана с экспериментами по рассеиванию альфа-частиц при прохождении их через вещество. Альфа-частицы являются ядрами атомов гелия и имеют положительный электрический заряд, так как состоят из двух протонов и двух нейтронов. Английский ученый Резерфорд, пропуская альфа-частицы с большой кинетической энергией через тонкие металлические пластинки, установил, что большая часть частиц отклоняются от первоначального направления на небольшие углы. Наряду с рассеиванием на малые углы, было обнаружено отклонение отдельных частиц и на большие углы, доходящие до 1800 (Рис.1). Такое рассеивание было обнаружено и при прохождении альфа-частиц через газы.
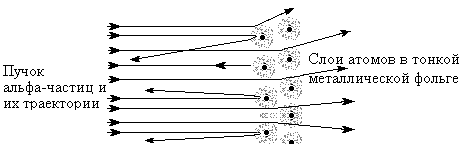 |
Рис.1. Схема опытов Резерфорда.
При анализе этих экспериментов было установлено, что отклонения происходят вследствие кулоновского отталкивания от положительного заряда, сосредоточенного в очень малом объеме внутри атома. До этого уже было известно (по экспериментам с ионизацией газов), что в составе атомов вещества также имеются элементарные частицы – электроны (с малой массой и отрицательным зарядом). Для объяснения результатов рассеивания Резерфорд в 1911г. предложил планетарную модель атома. Согласно этой модели атом построен по типу Солнечной системы - в центре атома в очень малой области (10-14 м) находится положительно заряженное ядро, в котором сосредоточена почти вся масса атома, а вокруг ядра под действием сил Кулоновского притяжения двигаются по замкнутым орбитам электроны (примерный радиус орбит -10-10м). При этом суммарный заряд электронов равен по величине заряду ядра, поэтому в целом атом нейтрален. При прохождении альфа-частиц через такой атом, только малая часть частиц будет сталкиваться с ядром и рассеиваться назад, основная их часть будет проходить на больших расстояниях от ядра и, вследствие малости Кулоновских сил, будут отклоняться на небольшие углы.
Таким образом, планетарная модель атома полностью объяснила эксперименты по рассеиванию. Однако, согласно классической электродинамике электрон, двигающийся по орбите вокруг ядра должен испускать электромагнитные волны непрерывного спектра частот. При этом он теряет свою энергию и через малый интервал времени (10-8 с) должен упасть на ядро, то есть такой атом нестабилен и имеет очень малое время жизни. Но, как известно, атомы отличаются большим временем жизни. Кроме того, из экспериментов по изучению частотного состава излучения (спектров) отдельных атомов в газах, известно, что атомы в невозбужденном (нормальном) состоянии не испускают электромагнитные волны, они излучают их только после передачи им энергии (при возбуждении), при зтом спектр частот имеет дискретный характер. Например, у атома водорода было обнаружено несколько серий частот излучения, наиболее известные описываются соотношениями:
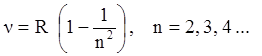 (1.1)
(1.1)
серия Лаймана для ультрафиолетового излучения,
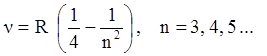 (1.2)
(1.2)
серия Бальмераа для видимого излучения
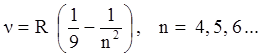 (1.3)
(1.3)
серия Пашена для инфракрасного излучения, здесь R-постоянная Ридберга, n – номер частоты (номер линии спектра излучения) в серии. Эксперименты по изучению спектра поглощения электромагнитного излучения для атома водорода показали, что спектр поглощения тоже имеет дискретный характер, описываемый соотношениями (1.1‑1.3). Подобная дискретность спектров была обнаружена у всех атомов. Таким образом, планетарная модель атома требовала серьезных доработок.
Для объяснения спектров излучения и поглощения атома водорода в 1913г. датский ученый Бор добавил к этой модели три ограничения (постулата), которые не соответствовали законам классической механики.
1. Атом может находиться в различных состояниях, в этих состояниях электрон двигается по определенным стационарным орбитам без излучения и без потери энергии. Эти орбиты называют Боровскими орбитами.
2. При движении по Боровским орбитам электрон имеет строго определенный (дискретный) момент импульса L (L равен произведению массы электрона, его скорости и радиуса орбиты). Его значение задается формулой квантования Бора
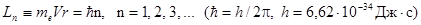 ,
,
где момент импульса связывается с постоянной Планка h и квантовым числом n.
Квантовое число n является номером состояния атома и номером Боровской орбиты электрона. В этих состояниях радиусы орбит электрона и его скорости различны, атом также имеет различные энергии. Обычно атом находится в основном или невозбужденном состоянии n=1 с наименьшим значением энергии, состояния с n = 2, 3, 4 имеют большие энергии и называются возбужденными.
3. При передаче атому энергии он переходит в какое-либо возбужденное состояние с n = 2, 3, 4… (если передача энергии производится с помощью электромагнитного излучения, то происходит поглощение атомом порции излучения), в возбужденном состоянии атом находится недолго (»10-8с), он испускает порцию (квант) электромагнитного излучения и переходит в какое-либо состояние с меньшим квантовым числом. При всех переходах, в соответствии с законом сохранения, энергия кванта e точно равна разности энергий атома e = En–Em.
При использовании этих постулатов, расчет полной энергии атома Е, которая складывается из кинетической энергии вращения электрона и потенциальной энергии электростатического взаимодействия электрона с ядром приводит к соотношению En = ‑ h R/n 2. Отсюда, используя формулу немецкого ученого Планка для кванта электромагнитного излучения e = h n и закон сохранения энергии в виде e = En‑Em , можно получить n = (En‑Em)/ h = R(1/n2-1/n2), что полностью соответствует результатам экспериментов (1.1‑1.3). Таким образом, данная модель позволила рассчитывать и объяснять спектры атома водорода, за что в 1922 г. Бор был удостоен Нобелевской премии по физике. Изложенная выше теория была обобщена (Теория Бора-Зоммерфельда, 1915г.) и для описания "водородоподобных" атомов, содержащих один электрон, движущийся в поле ядра с положительным зарядом (таких как однократно ионизированный гелий, двукратно ионизированный литий, трехкратно ионизированный бериллий и т.д.), но для более сложных атомов она оказалась непригодной.
Вторая серия необычных явлений связана с прохождением элементарных частиц через неоднородные среды, при котором наблюдаются явления дифракции и интерференции. Например, при рассеянии электронов от поверхности монокристалла никеля получается отчетливая дифракционная картина (опыт Дэвиссона и Джермера). Дифракция пучка электронов при прохождении через тонкие слои металлов и кристаллов была обнаружена Томсоном (Рис.2). Позднее было обнаружено, что аналогичное явление дифракции наблюдается также для протонов, нейтронов и даже для молекул водорода при их попадании на кристалл.
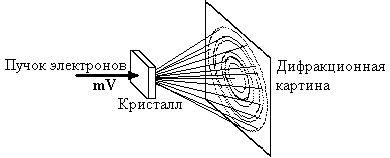 |
Рис.2. Схема эксперимента Томпсона по дифракции электронов.
Обнаружена была и интерференция элементарных частиц. Например, если направить пучок электронов на две щели, то на экране из фотоимульсии после проявления можно наблюдать интерференционную картину в виде параллельных полос, расположенных на одинаковом расстоянии друг от друга (Рис.3). Интересно, что при малых интенсивностях электронных пучков, наблюдается постепенное формирование интерференционной картины (Рис.3.а – время пропускания мало, Рис.3.б – время пропускания большое), что доказывает корпускулярность электронов. Аналогичные результаты были получены и при интерференции других частиц.

Рис.3. Схема экспериментов по интерференции электронов.
Таким образом, элементарные частицы в одних условиях проявляют свойства волн (явления дифракции, интерференции), в других же – свойства отдельных частиц‑корпускул (движение электронов в электронно-лучевой трубке, взаимодействие электрона и фотона при фотоэффекте и эффекте Комптона), что не может быть объяснено в рамках классической механики.
1.2.Гипотеза Луи-де-Бройля о корпускулярно-волновом дуализме свойств микрочастиц. @
Как известно, эксперименты с электромагнитными волнами показали, что в некоторых явлениях они проявляют свойства частиц (фотоэффект, эффект Комптона, тепловое излучение и др). Эти явления удалось описать, если предположить согласно теории Планка, что электромагнитное излучение является потоком частиц‑фотонов или квантов со следующими значениями энергии и импульса
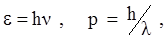 (1.4)
(1.4)
где n- частота, l- длина волны.
По аналогии, Луи де Бройль в 1923 году выдвинул гипотезу, что для объяснения волновых свойств микрочастиц им необходимо сопоставить особые волны, которые были названы волнами де Бройля. То есть, если микрочастице приписать некоторый волновой процесс с длиной волны
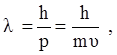 (1.5)
(1.5)
(где р, m, υ – импульс, масса и скорость частицы), то по формулам дифракции и интерференции для электромагнитных волн можно рассчитать эти явления и для пучков микрочастиц. Например, по известной формуле оптики для дифракционной решетки dSin(ak) = kl можно рассчитать положения максимумов и при дифракции микрочастиц. Эта гипотеза нашла полное подтверждение в вышеупомянутых экспериментах.
Эксперименты также показали, что распространение волн де Бройля не связано с распространением электромагнитных волн, а также каких-либо других волн, известных в классической физике. Наблюдаемое постепенное формирование интерференционной картины показывает, что волны де Бройля связаны со статистической природой движения микрочастиц и имеют вероятностное истолкование.
1.3.Соотношение неопределенностей Гейзенберга.@
Своеобразие движения микрочастиц, как оказалось, заключается также и в том, что ее траекторию нельзя характеризовать точными значениями координат и скорости (т.е. нельзя определить одновременно положение микрочастицы в пространстве и ее скорость с произвольной точностью). Немецкий ученый Гейзенберг в 1927г. установил, что неопределенности или погрешности измерения координаты Δх, Δy, Δz и импульса Δрх, Δрy, Δрz удовлетворяют соотношениям:
Δх Δрх ≥ h, Δy Δрy ≥ h, Δz Δрz ≥ h. (1.6)
Подобное соотношение имеется и для неопределенности измерения времени состояния микросистемы Δt и ее энергии ΔЕ
Δt ΔЕ≥h, (1.7)
все эти формулы называются соотношениями неопределенностей Гейзенберга.
Наличие этих соотношений объяснятся тем, что при измерении одного параметра микрочастицы, второй соответствующий параметр искажается измерительным прибором и чем точнее измеряется один, тем больше искажается второй. Это происходит и для макрообъектов, но вследствие их больших масс воздействие приборов оказывается несущественным. Например, при определении координат макрообъекта путем локации используют поток фотонов, которые испускаются локатором, они со скоростью света долетают до объекта, отражаются от него и возвращаются назад. Зная время движения фотона и его скорость можно легко определить расстояние до объекта, причем вследствие массивности макрообъекта, его скорость изменится незначительно. Если же использовать принцип локации для определения координаты микрочастицы, то при отражении от нее фотона он передаст ей импульс, сравнимый с импульсом частицы, что приведет к значительному изменению ее скорости. Подобные изменения соответствующих параметров происходят также при измерении скорости, энергии, времени.
Соотношения неопределенностей позволяют определить границы применимости понятий и законов классической механики к объектам, т.е. возможности одновременного использования понятий координаты и скорости при описании движения. Учитывая, что рх = mvx, можно получить Δх Δvх ≥ h/m, откуда следует, что чем больше масса частицы, тем меньше неопределенность ее координаты и скорости и, следовательно, с тем большей точностью можно применять к этой частице понятие траектории. Для пояснения рассмотрим два примера.
1. Рассмотрим пылинку массой m=10-12 кг и линейными размерами 10-6м и определим для нее неопределенность скорости (неопределенность определения ее координаты примерно равна сотой доли ее размера т.е. Δх = 10-8м). Согласно соотношениям неопределенностей Δvх = h/mΔx = 6,62∙10-34/(10-12∙10-8) = 6,62∙10-14м/с. В результате получается неопределенность измерения скорости, намного меньшая скорости, с которой пылинка может двигаться. Поэтому, в данном случае, скорость и импульс можно определить практически точно и поэтому для пылинки можно использовать понятие траектории и законы классической механики.
2. Рассмотрим электрон, движущийся в атоме водорода. Неопределенность его координаты порядка размера самого атома, т.е. Δx = 10-10м. Определим Δvх: Δvх = h/mΔx = 6,62∙10-34/(9, 1∙10-31∙10-10) = 7,3∙106м/с. Если рассчитать скорость электрона в атоме согласно классической механики, учитывая, что роль центростремительной силы играет сила Кулона, то скорость получается порядка 2∙106м/с и в данном случае неопределенность измерения скорости оказывается больше самой скорости. Поэтому нельзя говорить о движении электрона в атоме по определенной траектории.
1.4.Постулаты квантовой механики. Вероятностный характер движения частиц. Волновая функция, её статистический смысл. Задание состояния микрочастицы.@
Объяснить одновременное наличие корпускулярных и волновых свойств у микрочастиц удалось на основе идей Бора и Луи-де-Бройля в рамках новой теории, называемой волновой или квантовой механикой, созданной Гейзенбергом, Шредингером, Борном и многими другими учеными начала ХХ века. Квантовая механика базируется, как и любая другая физическая теория, на ряде постулатов. Основные постулаты можно представить упрощенно в следующем виде.
1. Движение микрочастиц в пространстве имеет вероятностный (стохастический) характер. Это относится не только к совокупности (ансамблю) частиц, но и к каждой отдельной частице. Согласно этому постулату, микрочастица, находясь в силовых полях или в вакууме (при отсутствии полей), испытывает такое воздействие, что нельзя в любой момент времени определить точно параметры ее движения. Например, нельзя одновременно характеризовать ее траекторию точными значениями координат и скорости или точными значениями энергии и времени какого-либо процесса у частицы.
2.Стохастический характер движения микрочастиц требует применения понятий математики теории вероятности для описания и расчета определенных значений параметров частиц в эксперименте. С точки зрения математики, отсюда следует, что движение таких частиц должно описываться с помощью некоторой «особой» волновой функции, которая должна характеризовать вероятностные особенности микрочастиц. Интерпретацию волновой функции дал в 1926г. немецкий физик Макс Борн следующим образом - волновая функция ψ (х, у, z) характеризует вероятность нахождения частицы в данный момент времени в некоторой точке пространства. Согласно Борну, физический смысл имеет не сама функция, а квадрат модуля волновой функции |ψ|2, который равен вероятности dP того, что частица будет обнаружена в пределах рассматриваемого малого объема dV. Формула связи этих понятий имеет вид
dP = |ψ|2 dV = |ψ|2dxdydz. (1.8)
Для совокупности частиц под вероятностью понимают отношение числа частиц в малом объеме к общему числу частиц, а для одной частицы – отношение времени пребывания частицы в малом объеме к общему времени рассмотрения движения частицы.
3.Волновая функция является основной характеристикой состояния микрообъекта, с помощью волновой функции можно рассчитать вероятность пребывания частицы в различных точках пространства в различные моменты времени, а также средние значения различных ее параметров. Соответственно вероятностному смыслу волновой функции и используя формулы теории вероятности, средние значения параметров находятся путем усреднения соответствующих операторов с помощью волновой функции. Например среднее значение для модуля радиуса-вектора частицы <r> можно найти по формуле
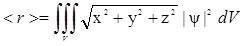 . (1.9)
. (1.9)
Так как в физических экспериментах определяются именно средние значения параметров частицы, то можно говорить, что состояние частицы полностью задается ее волновой функцией.
4.Вид волновой функции зависит от типа частицы и от внешних силовых полей, действующих на частицу. Вид функции находится с помощью специального дифференциального уравнения, называемого уравнением Шредингера.
5. Если в эксперименте наблюдается суперпозиция (объединение) микрочастиц, описываемых разными волновыми функциями, то объединенный ансамбль этих частиц будет описываться суммой их волновых функций. Например, если при интерференции микрочастиц на двух щелях, их можно по отдельности описать двумя функциями ψ1 и ψ2, тогда совокупность этих частиц в районе экрана должна описываться функцией ψ = ψ1+ψ2. Так как вероятность распределения частиц на экране dP определяется квадратом модуля волновой функции, то получаем dP» |ψ|2 = |ψ1|2 + 2|ψ1ψ2| + |ψ2|2. Отсюда следует, что распределение зависит не только от простого сложения вероятностей двух независимых ансамблей |ψ1|2 + |ψ2|2, но и от результата их специфичного квантового «взаимодействия» 2|ψ1ψ2|, вследствие чего и наблюдается интерференция частиц.
Имеется еще ряд постулатов, но они имеют более частный характер, о некоторых из них будет сказано далее.
1.5.Уравнение Шредингера. Физические ограничения на вид волновой функции. Стационарное уравнение Шредингера, стационарные состояния. @
Для расчета волновой функции необходимо иметь уравнение, которое позволяло бы для любого момента времени определить эту функцию с учетом действующих на частицу внешних силовых полей. Чтобы искомое уравнение учитывало волновые свойства микрочастиц, необходимо чтобы оно по форме было волновым уравнением, подобно тем, которые описывают звуковые или электромагнитные волны. Известно, что для плоской волны, распространяющейся вдоль оси х, волновое уравнение – это дифференциальное уравнение в частных производных, где независимыми переменными являются координаты и время. Учитывая такие аналогии, австрийский физик Эрвин Шредингер получил в 1926 г. основное уравнение квантовой механики для ψ (х, у, z, t)
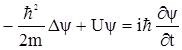 , (1.10)
, (1.10)
где m – масса частицы, i – мнимая единица, U – потенциальная энергия частицы, Δ‑оператор Лапласа, который представляет собой сумму вторых частных производных по координатам, т.е.
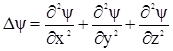 (1.11)
(1.11)
Из уравнения Шредингера следует, что конкретный вид волновой функции зависит от потенциальной энергии U, т.е. определяется характером сил, действующих на частицу. Уравнение Шредингера оказалось комплексным (включающим в себя мнимую единицу), поэтому и волновая функция также комплексная, при этом реальный физический смысл имеет квадрат модуля волновой функции (2.5, 2.6), который всегда действителен.
Уравнение Шредингера, будучи дифференциальным уравнением, может иметь множество решений. Из этих решений смысл имеют только те, в которых волновая функция будет однозначной, непрерывной и конечной, что соответствует физической реальности. Эти требования должны относиться и к частным производным от функции по времени и координатам, так как они тоже входят в уравнения Шредингера. Кроме этих требований на волновую функцию накладывается условие нормировки
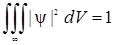 , (1.12)
, (1.12)
которое следует из того факта, что частица реально существует и обязательно находится где-либо в окружающем пространстве. Поэтому суммарная вероятность нахождения частицы во всем бесконечном пространстве равна единице, т.е. это достоверное событие. Смысл и назначение уравнения Шредингера заключается в том, что если известна волновая функция некоторой частицы в начальный момент времени и известно силовое поле, в котором она движется, то, решив это уравнение, можно найти волновую функцию и узнать характеристики состояния частицы в последующие моменты времени.
Если силовое поле, в котором движется частица, постоянно во времени, то U не зависит от времени и волновую функцию можно представить в виде 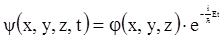 , где Е – полная энергия частицы. Если мы подставим такую функцию в уравнение Шредингера, проведем дифференцирование и сокращение, то получим уравнение
, где Е – полная энергия частицы. Если мы подставим такую функцию в уравнение Шредингера, проведем дифференцирование и сокращение, то получим уравнение
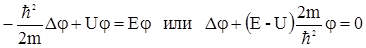 (1.13)
(1.13)
Это - уравнение Шредингера для, так называемых, стационарных состояний, находясь в которых частица имеет определенные, не меняющиеся со временем характеристики.
1.6.Частица в одномерной бесконечно глубокой потенциальной яме. Квантование энергии частицы. Объяснение туннельного эффекта. Гармонический осциллятор.@
Для выяснения особенностей решения уравнения Шредингера, рассмотрим поведение микрочастицы в одномерной бесконечно глубокой потенциальной «яме». Такой вид потенциала взаимодействия в природе не наблюдается, но он наиболее простой и может демонстрировать основные особенности решения (наиболее близок он к потенциалу, используемому при рассмотрении поведения электрона в металле). Такая потенциальная «яма» описывается следующими соотношениями для потенциальной энергии (рис.4):
U = ¥ в областях 1, 3 для x < 0 и x > a; U = 0 в области 2 для 0> x >a.
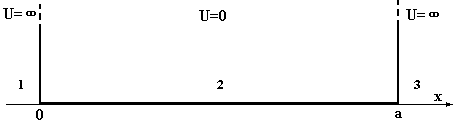
Рис.4. График потенциала одномерной бесконечно глубокой «ямы».
Запишем стационарное уравнение Шредингера для областей 1, 3, где U=¥

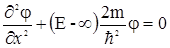 , (1.14)
, (1.14)
его единственно возможное решение j=0. Это означает, что вероятность нахождения частицы в этих областях равна нулю и частица туда проникнуть не может.
Для области 2 стационарное уравнение Шредингера имеет вид
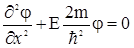 , (1.15)
, (1.15)
из теории дифференциальных уравнений следует, что его решение имеет вид
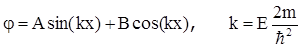 . (1.16)
. (1.16)
Вследствие требования непрерывности функции j, она должна быть равна нулю в точках x=0 и x=a, что следует из решения для областей 1, 3. Отсюда получается, что должны выполняться соотношения Asin(0)+Bcos(0)=0, Asin(ka)+Bcos(ka)=0 и, согласно математике, это будет при B=0 и ka=pn, где n-целое число. Необходимое также условие нормировки (1.12) в данной задаче имеет вид
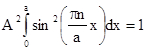 , (1.17)
, (1.17)
взяв этот интеграл, получаем 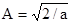 и в результате имеем конечное выражение для возможных решений уравнения Шредингера в поставленной задаче
и в результате имеем конечное выражение для возможных решений уравнения Шредингера в поставленной задаче
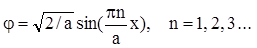 . (1.18)
. (1.18)
Данное решение показывает, что поведение микрочастицы в одномерной бесконечно глубокой потенциальной «яме» может быть различным в зависимости от значения числа n, его называют квантовым числом и рассматривают как номер возможного состояния микрочастицы.
Рассмотрим графики функции j2 (рис.5), которая согласно (1.8) определяет вероятность нахождения частицы в разных точках «ямы» для различных состояний.
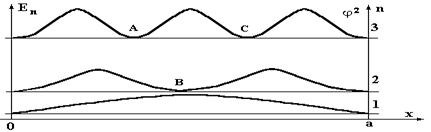
Рис.5. Графики вероятности нахождения частицы в бесконечно глубокой потенциальной «яме» для n = 1, 2, 3. Горизонтальные, тонкие линии соответствуют значениям энергий состояний (энергетическая диаграмма или уровни возможных энергий системы), толстые линии соответствуют функции j2.
Из рисунка 5 видно, что во втором и в третьем состояниях микрочастица не может находиться в некоторых точках «ямы» A,B,C, однако она может находиться между этими точками. Кроме этого, видно, что минимальное значение полной энергии Е1, которая в области 2 является кинетической энергией, не равна нулю, это означает что частица находится в непрерывном движении. Такое поведение микрочастицы существенно отличается от поведения макрочастиц и приводит к тому, что в квантовой механике не может быть использовано классическое понятие траектории.
Используя найденные соотношения ka = pn и (1.16), получим выражение для полной энергии частицы
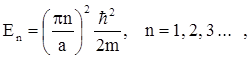 (1.19)
(1.19)
которое показывает, что энергия частицы в разных состояниях различна и строго определена (имеет дискретный спектр). Других значений энергии частица иметь не может, возможные дискретные значения называют квантовыми уровнями энергии. Подобное квантование у микрочастиц может происходить и с другими параметрами: импульсом, моментом импульса.
Если рассмотреть таким же образом более реальную ситуацию, когда частица находится в одномерной потенциальной «яме» конечной глубины (U = Uo в областях 1,3 для x < 0 и x > a; U = 0 в области 2 для 0 > x > a), то, в отличие от случая бесконечно глубокой ямы, функция j2 не будет равна нулю в областях 1, 3 даже при малых энергиях частицы (рис.6).
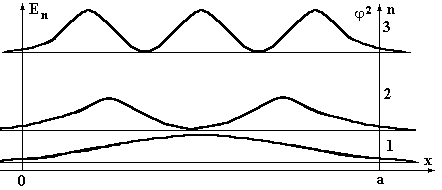
Рис.6. Графики вероятности нахождения частицы в потенциальной «яме» конечной глубины для n = 1, 2, 3.
Это означает, что частица может выйти за пределы потенциальной «ямы» даже в случае, когда ее энергия меньше Uo, чего в классической механике происходить не может. Подобное явление наблюдается и при рассмотрении поведения микрочастицы вблизи одномерного потенциального «барьера» (U = 0 в областях 1,3 для x < 0 и x > a; U = Uo в области 2 для 0 > x > a). Если решить уравнение Шредингера в этом случае, то можно обнаружить, что частица с энергией меньшей Uo может проходить сквозь этот «барьер».
Такие явления прохождения сквозь потенциальные барьеры частиц с малой энергией являются чисто квантовыми и называются «туннельными эффектами». Экспериментально эти явления наблюдаются с микрочастицами в различных ситуациях: автоэлектронная эмиссия – выход электронов за пределы металлов при малых температурах, автоионизация – выход электронов из атомов и молекул под действием слабого электрического поля, когда энергии поля бывает недостаточно для вырывания электрона с точки зрения классической механики. В физике элементарных частиц подобное явление наблюдается в радиоактивном излучении при выходе альфа частиц из ядер атомов.
Очень важным для атомной физики является рассмотрение поведения микрочастицы в силовом поле, когда потенциальная энергия зависит от координаты x в соответствии с законом 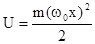 , этот случай соответствует в классической механике гармоническим колебаниям тела массой m с циклической частотой wo (гармонический осциллятор). Примерно такие колебания в мире микрочастиц происходят при движении атомов в молекуле, а также при колебаниях молекул около узлов кристаллической решетке в твердых телах.
, этот случай соответствует в классической механике гармоническим колебаниям тела массой m с циклической частотой wo (гармонический осциллятор). Примерно такие колебания в мире микрочастиц происходят при движении атомов в молекуле, а также при колебаниях молекул около узлов кристаллической решетке в твердых телах.
Date: 2015-05-18; view: 741; Нарушение авторских прав