Собственные значения волновой функции

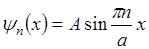
А определяется с помощью условия нормировки:

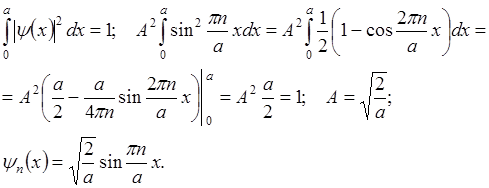
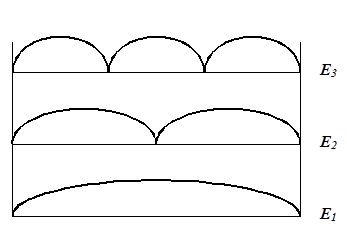
Рассмотренная задача является моделью потенциального поля атома или молекулы. Изолированный атом является потенциальной ямой, в которой электрон может занимать одно из дискретных энергетических значений. Каждому квантовому состоянию волновой функции соответствует значение полной энергии частицы (квантование энергии).

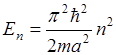
Частица в прямоугольном трехмерном потенциальном ящике.

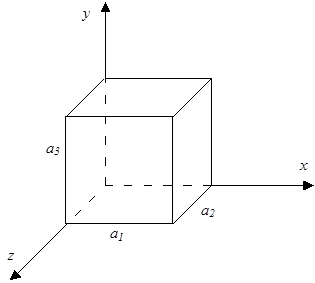
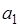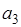Обозначим G{0<x< ,0<y< ,0<z< 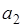} внутренняя область параллелепипеда. Потенциальная энергия в точке М(х, у, z) имеет вид:

Вне потенциального ящика волновая функция равна нулю.

Внутри потенциального ящика 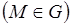волновая функция может быть найдена как решение стационарного уравнения Шрёдингера:

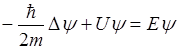
Это решение имеет вид:

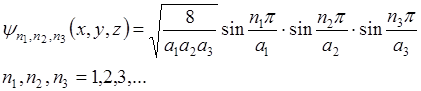
Квантовое состояние частицы, находящейся в потенциальном ящике, определяется тремя квантовыми числами . Каждому квантовому состоянию соответствует определенное значение энергии частицы.

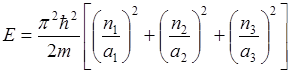
Только при этих значениях полной энергии частицы уравнение Шрёдингера имеет регулярные решения.

Понятие о вырождении энергетических уровней.

Если 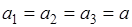, то есть для потенциального ящика кубической формы, когда задача обладает пространственной симметрией за счет равноправия всех трех межпространственных направлений, существуют квантовые соотношения (например

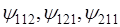), находясь в которых частица имеет одинаковые значения полной

энергии.

Совокупность таких состояний, в которых частица имеет одинаковые значения полной энергии Е, называют вырожденными состояниями, а число состояний, соответствующих данному значению Е, называется кратностью или степенью вырождения.

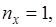
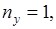
Например: 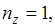тогда 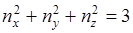так как нельзя подобрать три другие целые числа, сумма квадратов которых равна 3, то этому состоянию (1, 1, 1) соответствует только одно значение энергии.

Но если 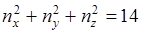, то соответствует значение энергии

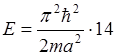
nx	ny	nz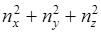

Этому значению энергии соответствует шесть различных состояний. Такие состояния вырожденные, а число совпадающих уровней энергии называется квантовым весом состояния. В первом случае квантовый вес равен 1, а во втором - 6. Кратность вырождения равна 6.

Одномерный потенциальный барьер.

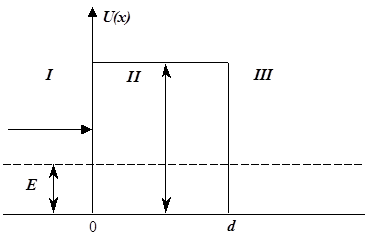
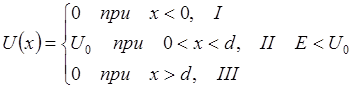
Существует отличная от 0 вероятность того, что частица преодолеет такой высокий потенциальный барьер (туннельный эффект).

I.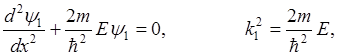

II.

III.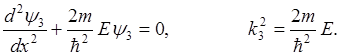

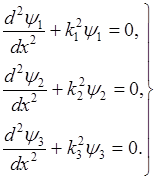
Частные решения в комплексном виде: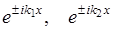

Плоские волны де Бройля.

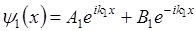
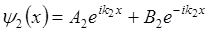
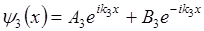
где 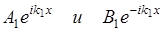характеризуют падающую и отраженную волну (точка x=0).

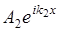- волна, прошедшая в область II или падающая на границу (x=0).

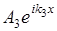- волна, прошедшая в область Ш.

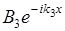- отраженная волна, идущая из бесконечности.

В области III имеет место только одна волна, прошедшая через порог, то коэффициент .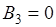

Вероятность нахождения частицы через потенциальный порог характеризуется коэффициентом прозрачности D, который равен отношению интенсивности прошедшей волны к интенсивности падающей волны:

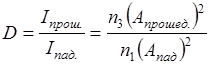
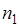- показатель преломления для области I.

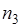- показатель преломления для области Ш.

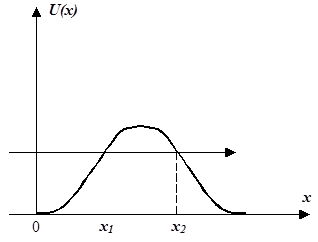
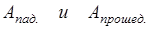- амплитуды падающей и прошедшей волны.

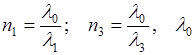- длина световой волны в вакууме.

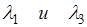- в средах с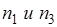

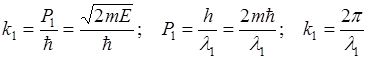
Для областей I и III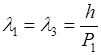

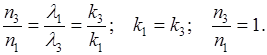
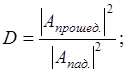
Условие непрерывности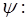

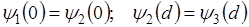тогда

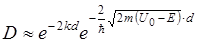
При E<U₀ вопреки выводам классической механики, частицы проходят через потенциальный барьер, причем вероятность прохождения с увеличением Е возрастает, а при увеличении d потенциальный барьер уменьшается.

Для потенциального барьера произвольной формы (рис.) коэффициент прозрачности определяется:

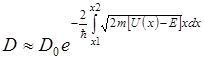
Прохождение частицы через потенциальный барьер называется туннельным эффектом. Теория туннельного эффекта позволяет объяснить автоэлектронную эмиссию электронов из металла, работу туннельных полупроводниковых диодов, - распад.

Потенциальная стенка (потенциальный порог)

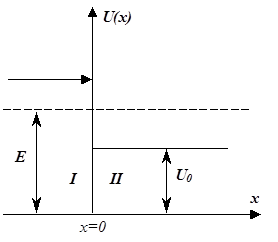
Рассматривается случай движения частицы, когда потенциальная энергия U(x) меняется скачком в одной точке, то есть когда потенциальная кривая U=U(x) имеет вид ступеньки высотой U₀

U(x)=0, x<0,

U(x)=U₀, x>0.

Потенциальный барьер бесконечной ширины.

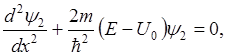
Общее решение:

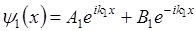
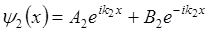, где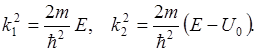

Рассматривается условия перехода частицы из области I в область II в двух случаях:

1)E>U₀, полная энергия частицы больше высоты потенциального барьера.

2)E<U₀

При E>U₀ классическая частица обязательно перейдет из области I в область II и будет двигаться в ней с кинетической энергией E-U₀.

Квантовая частица на границе частично отразится, частично перейдет в область в область II как свет. Вероятность отражения характеризуется коэффициентом отражения

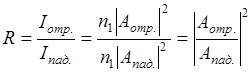
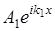- падающая волна;

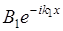- отраженная волна.

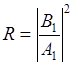- вероятность отражения на границе x=0.

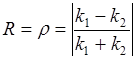
В области I кинетическая энергия электрона Е и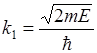

Если E>U- потенциальный барьер называется низким, E<U- высоким.

В области II кинетическая энергия электрона равна (E-U) и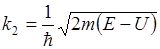

Коэффициент отражения

Разделим числитель и знаменатель на :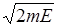

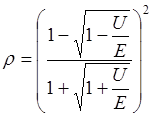
Решая уравнение относительно 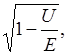получим

Возведя обе части уравнения в квадрат, определим высоту потенциального барьера:

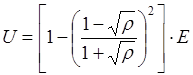
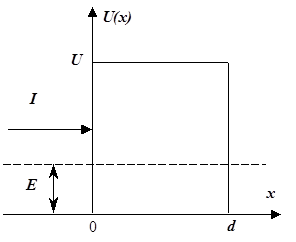
Если E<U, то вероятность прохождения W частицы через потенциальный барьер совпадает по физическому смыслу с коэффициентом прозрачности D (W=D)

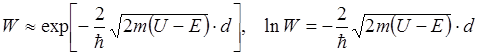
Изменяя знак у правой и левой части, найдем d.

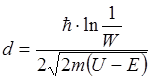
Коэффициент преломления n волны де Бройля на границе низкого потенциального

барьера бесконечной ширины 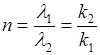, где 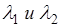- длины волн де Бройля в областях I и II (частица движется из области I в область II); 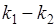- соответствующие значения волновых чисел.

Коэффициенты отражения 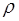и пропускания 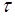волн де Бройля через низкий (U-E) потенциальный барьер бесконечной ширины:

.

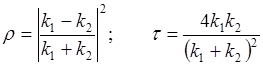
Коэффициент прозрачности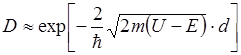

Если барьер произвольной формы: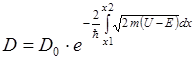

Гармонический осциллятор. Фотоны.

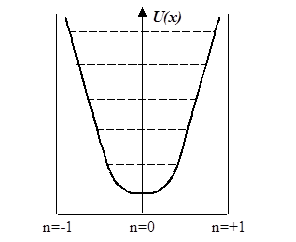
Одномерный гармонический осциллятор - это частица, совершающая движение под действием квазиупругой силы .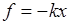

Потенциальная энергия такой частицы имеет вид:

Соответствующая потенциальная кривая есть парабола, которая образует что-то вроде ящика с отражающими стенками. Стационарное уравнение Шредингера:

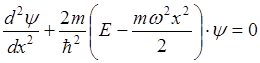
Это уравнение имеет регулярные решения только при значениях энергии

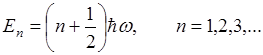
Уровни энергии отстоят друг от друга на одинаковом расстоянии, равном 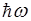. Наименьшее значение энергии 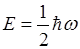называют нулевой энергией осциллятора, она не исчезает и при абсолютном нуле температуры (T=0). Внутри такого ящика возникают стоячие волны.

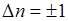переходы возможны лишь между соседними уровнями. Это так называемое правило отбора, которое показывает, что энергия может изменяться только порциями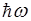

Обозначим 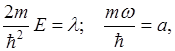тогда

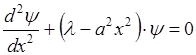
Если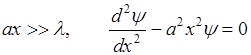

Дифференциальное уравнение второго порядка с постоянными коэффициентами. Решение его:

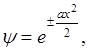
Надо взять только со знаком «-», так как со знаком «+» функция безгранично растет:

.

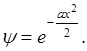Математический аппарат квантовой механики.

Оператор показывает, какое действие необходимо произвести над функцией.

Оператор Лапласа -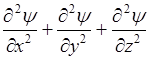

жаждет дважды продифференцировать .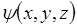

Оператор координаты показывает, что волновую функцию нужно умножить на координату.

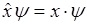
Оператор проекции импульса жаждет продифференцировать волновую функцию 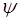по x.

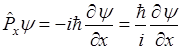
Оператор энергии показывает, что волновую функцию нужно дважды продифференцировать

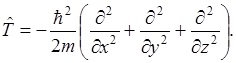
Оператор Гамильтона 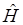изображает полную энергию системы.

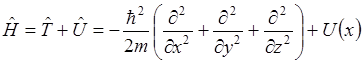
Обычно в квантовой механике используют линейные самосопряжённые операторы .

Оператор 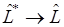сопряжён оператору 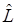, если скалярные произведения двух функций равны

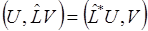
Если оператор сопряжённый данному совпадает с ним самим, т. е.

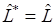
в таком случае оператор называется самосопряжённым (ирмитовым).

Теорема: Собственные значения ирмитова оператора всегда действительны.

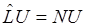
т. е. если 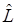ирмитов оператор, то произведение на U равно действительному числу. Волновая функция, описывающая состояние системы, часто находится из операторного уравнения:

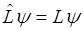(1)

Собственные значения и собственные функции линейных операторов определяются из уравнения (1)

В результате применения 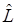к функции 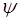иногда получается вновь та же функция, умноженная на некоторое число L.

В квантовой механике главным уравнением является уравнение Шредингера:

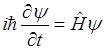
Для стационарных процессов

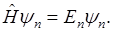
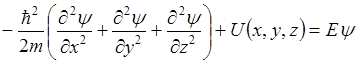
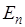- собственные значения оператора Гамильтона.

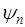- собственные функции.

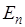- могут принимать как дискретные, так и непрерывные значения.

Собственные значения 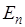и собственные значения 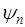находятся из решения уравнения

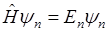
Если одному уровню энергии соответствует несколько собственных функций или состояний, то такие уровни называются вырожденными.

Число состояний соответствующих данной энергии, называются кратностью вырождения и статистическим весом

g(E).

Оператор кинетической энергии

Оператор потенциальной энергии есть оператор умножения.

.

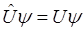
Основные операторы квантовой механики:

Динамические переменные квантовой механики	Оператор квантовой механики
Координата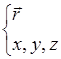
Импульс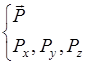
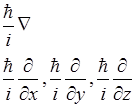
Момент количества движения (момент импульса)
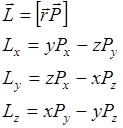
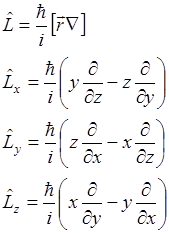
Энергия (в отсутствии магнитного поля)

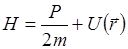
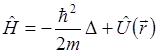
Date: 2015-05-18; view: 894; Нарушение авторских прав