Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Задача № 17
|
|
Частица массой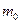 
движется в потенциальном поле, в котором её потенциальная энергия равна 
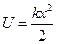(гармонический осциллятор). Оцените с помощью соотношения неопределённостей минимально возможную энергию частицы в этом поле.
Решение:
Энергия частицы равняется:
(1)
где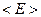 
- среднее значение энергии частицы, а 
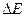- неопределённость энергии. Из выражения (1) видно, что минимальное значение энергии частицы, в случае 
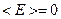, равняется по порядку величины её неопределённости 
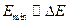. В этом случае неопределённость импульса частицы:
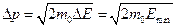(2)
С наибольшей степенью вероятности частица находится в области местонахождения классического осциллятора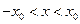 
, где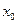 
- амплитуда колебаний классического осциллятора, которую определим, решая следующее уравнение:
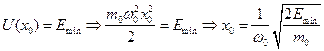(3)
где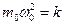 
.
Неопределённость частицы в этом потенциальном поле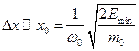 
. Воспользуемся первым соотношением неопределённостей Гейзенберга:
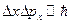(4)
Подставляя в уравнение (4) выражения, полученные для неопределённостей импульса и координаты, получим:
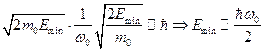(5)
Это значение соответствует нулевой энергии квантового гармонического осциллятора.
Ответ:
.
Date: 2015-05-18; view: 467; Нарушение авторских прав