Задача № 24

Частица находится в двумерной квадратной потенциальной яме с бесконечно высокими стенками во втором возбуждённом состоянии. Сторона ямы равна а. Определите вероятность нахождения частицы в области:

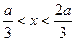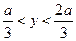а) ; б) ; в) .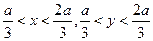

Решение:

Частица находится в потенциальной яме, имеющей следующий вид:

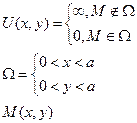
Составим уравнение Шредингера для области :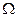

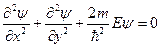(1)

или в виде:

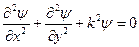(2)

где 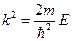. Решение этого дифференциального уравнения имеет вид:

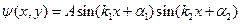(3)

Используем естественные условия, накладываемые на пси-функцию. Вне области 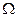частица находиться не может, поэтому её пси-функция вне области 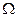равна нулю. Используя условие непрерывности, получим:

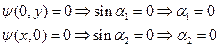
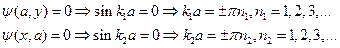
Тогда пси-функция примет вид:

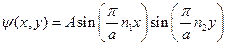(4)

Найдём вторые производные от пси-функции по x и по y:

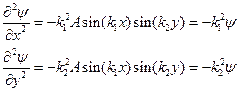(5)

Подставим эти производные в уравнение Шредингера (2):

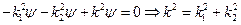(6)

Учитывая, что 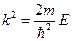, получим:

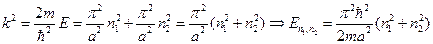(7)

Мы получили энергетический спектр частицы, находящейся в квадратной потенциальной яме с бесконечно высокими стенками. Из выражения (7) видно, что энергия частицы зависит от двух квантовых чисел 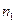и 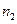. В таблице 1 приведены несколько возможных значени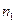й и 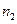и соответствующее им 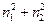, которое определяет значение энергии.

Таблица 1.

№ уровня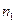

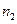
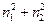
Как видно из таблицы, некоторые энергетические уровни вырождены, то есть существует несколько состояний, описываемых различными пси-функциями, но имеющими одно и то же значение энергии. Второму возбуждённому состоянию соответствуют квантовые числа 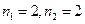(так как 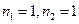соответствует основному состоянию, второй уровень – первое возбуждённое состояние, третий – второе возбуждённое состояние).

Определим константу A в выражении для пси-функции (4), используя условие нормировки:

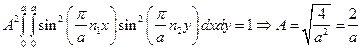(8)

Тогда пси-функции собственных состояний имеют вид:

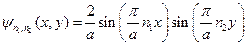(9)

Во втором возбуждённом состоянии:

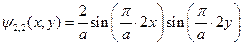(10)

Найдём функцию плотности вероятности нахождения частицы в единице объёма:

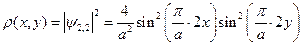(11)

Теперь определим искомые вероятности:

а)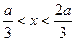

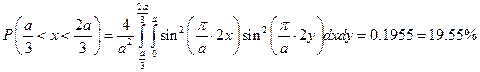
б)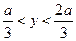

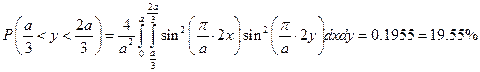
в)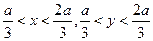

Ответ:

а) 19.55%; б) 19.55%; в) 3.8%.

Date: 2015-05-18; view: 461; Нарушение авторских прав