Задача № 7. Коллимированный пучок электронов, прошедших ускоряющую разность потенциалов , падает нормально на тонкую поликристаллическую фольгу золота

Коллимированный пучок электронов, прошедших ускоряющую разность потенциалов 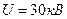, падает нормально на тонкую поликристаллическую фольгу золота. На фотопластинке, расположенной за фольгой на расстоянии 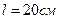от неё, получена дифракционная картина, состоящая из ряда концентрических окружностей. Радиус первой окружности 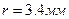. Определите: а) брэгговский угол 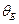, соответствующий первой окружности; б) длину волны де Бройля электронов 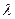; в) постоянную 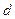кристаллической решётки золота.

Решение:

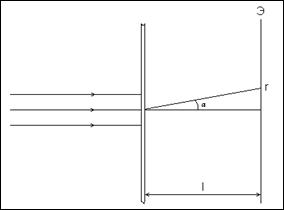
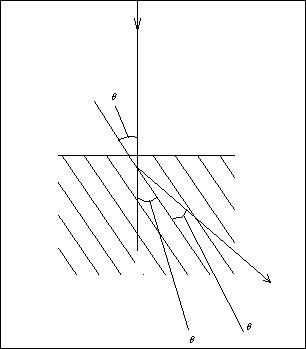
Рисунок 2 Рисунок 1

Используя рисунок 2, определим угол :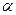

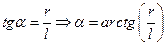(1)

Как видно из рисунка 1, угол 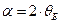, где 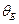- брэгговский угол скольжения. Таким образом, мы можем найти брэгговский угол, соответствующий первой окружности:

(2)

Длина волны де Бройля падающих на золотую фольгу электронов:

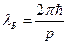(3)

где 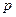- импульс электронов. Считая электроны релятивистскими, определим их импульс:

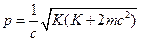(4)

где 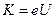- кинетическая энергия электрона, а 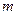- масса покоя электрона. Тогда дебройлевская длина волны электронов равняется:

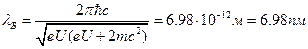(5)

Воспользуемся условием Вульфа-Брэггов:

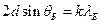(6)

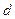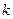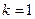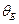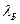где - постоянная кристаллической решётки, - порядок максимума (в нашем случае максимум первого порядка ). Найдём из выражения (6) постоянную кристаллической решётки, учитывая, что значение и определяются соответственно выражениями (2) и (5):

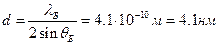(7)

Ответ:

а)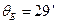

б)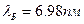

в) .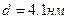

Date: 2015-05-18; view: 937; Нарушение авторских прав