Линзы. Преломление изображения в линзах

Преломление в линзе. Фокусы линзы. В гл. IX был сформулирован закон преломления света, устанавливаю­щий, как меняется направление светового луча при пере­ходе света из одной среды в другую. Был рассмотрен про­стейший случай преломления света на плоской гра­нице раздела двух сред.

В практических применениях очень большое значение имеет преломление света на сферической границе раздела. Основная деталь оптических приборов — линза — представляет собой обычно стеклянное тело, ограниченное с двух сторон сферическими поверхностями; в частном слу­чае одна из поверхностей линзы может быть плоскостью, которую можно рассматривать как сферическую поверх­ность бесконечно большого радиуса.

Линзы могут быть изготовлены не только из стекла, но, вообще говоря, из любого прозрачного вещества. В некото­рых приборах, например, применяются линзы из кварца, каменной соли и др. Заметим, что и поверхности линз могут быть также более сложной формы, например цилиндриче­ские, параболические и т. д. Однако такие линзы приме­няются сравнительно редко. В дальнейшем мы ограничимся рассмотрением линз со сферическими поверхностями.

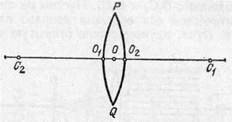
Рис. 193. Тонкая линза: О — оптический центр, С₁ и С₂ — центры огра­ничивающих линзу сферических поверхностей

Итак, рассмотрим линзу, ограниченную двумя сфериче­скими преломляющими поверхностями PO ₁ Q и PO ₂ Q (рис. 193). Центр первой преломляющей поверхности PO ₁ Q лежит в точке С ₁, центр второй поверхности PO ₂ Q — в точ­ке С ₂. На рис. 193 для ясности изображена линза, имеющая заметную толщину O ₁ O ₂. В действительности мы будем обычно предполагать, что рассматриваемые линзы очень тонки, т. е. расстояние О ₁ О ₂ очень мало по сравнению с O ₁ C ₁ или О ₂ С ₂. В таком случае точки О ₁ и O ₂ можно счи­тать практически сливающимися в одной точке О. Эта точка О называется оптическим центром линзы.

Всякая прямая, проходящая через оптический центр, называется оптической осью линзы. Та из осей, которая проходит через центры обеих преломляющих поверхностей линзы, называется главной оптической осью, остальные — побочными осями.

Луч, идущий по какой-либо из оптических осей, проходя через линзу, практически не меняет своего направления. Действительно, для лучей, идущих вдоль оптической оси, участки обеих поверхностей линзы можно считать параллельными, а толщину линзы мы считаем весьма малой. При прохождении же через плоскопараллельную пластинку, как мы знаем, световой луч претерпевает параллельное смеще­ние, но смещением луча в очень тонкой пластинке можно пренебречь (см. упражнение 26 после гл. IX).

Если на линзу падает световой луч не вдоль одной из ее оптических осей, а по какому-либо другому направлению, то он, испытав преломление сначала на первой ограничи­вающей линзу поверхности, потом на, второй, отклонится от первоначального направления.

Прикроем линзу черной бумагой 1 с вырезом, оставляю­щим открытым небольшой участок около главной оптиче­ской оси (рис. 194). Размеры выреза мы предполагаем малы­ми по сравнению с O ₁ С ₁ и O ₂ С ₂. Пустим на линзу 2 вдоль главной оптической оси ее слева направо параллельный пучок света. Лучи, идущие сквозь открытую часть линзы,

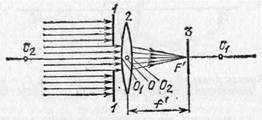
Рис. 194. Главный фокус линзы

преломятся и пройдут через некоторую точку F', лежащую на главной оптической оси, справа от линзы на расстоянии f ' от оптического центра О. Если в точке F' расположить белый экран 3, то место пересечения лучей изобразится в виде яркого пятнышка. Эта точка F' на главной оптиче­ской оси, где пересекаются после преломления в линзе лучи, параллельные главной оптической оси, называется главным фокусом, а расстояние f^f'=OF' — фокусным расстоянием линзы.

Нетрудно показать, пользуясь законами преломления, что все лучи, параллельные главной оптической оси и про­ходящие через небольшую центральную часть линзы, после преломления действительно пересекутся в одной точ­ке, названной выше главным фокусом.

Рассмотрим луч РМ, падающий на линзу параллельно ее главной оптической оси. Пусть этот луч встречает первую преломляющую поверхность линзы в точке М на высоте h над осью, причем h гораздо меньше, чем С ₂ О и С ₁ O (рис. 195). Преломленный луч пойдет по направлению ММ' и, преломившись снова на второй ограничивающей линзу поверхности, выйдет из линзы по направлению M'F', составляющему с осью угол j. Точку пересечения этого луча с осью обозначим через F', а расстояние от этой точки до оптического центра линзы — через f '.

Проведем через точки М и М' плоскости, касатель­ные к преломляющим поверхностям линзы. Эти касатель­ные плоскости (перпендикулярные к плоскости чертежа) пересекутся под некоторым углом q, причем угол q весьма мал, так как рассматриваемая нами линза — тонкая. Вместо преломления луча PMM'F' в линзе мы, очевидно, можем

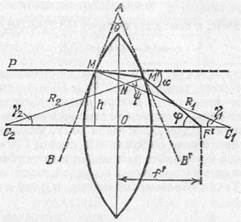
Рис. 195. Преломление в линзе луча РМ, параллельного главной оп­тической оси. (Толщина линзы и высота h изображены преувеличен­ными по сравнению с расстояниями R₁, R₂ и f''; в соответствии с этим и углы g₁ g₂ и q на рисунке чрезмерно велики.)

рассматривать преломление того же луча в тонкой призме ВАВ', образованной проведенными нами в точках М и М' касательными плоскостями.

Мы видели в § 86, что при преломлении в тонкой призме с преломляющим углом q луч отклоняется от первоначаль­ного направления на угол, равный

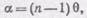(88.1)

где n есть показатель преломления вещества, из которого сделана призма. Очевидно, угол a равен углу j (рис. 195), т. е.

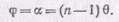(88.2)

Пусть C ₁ и С ₂ — центры сферических преломляющих по­верхностей линзы, a R ₁ и R ₂ — соответственно радиусы этих поверхностей. Радиус C ₁ M перпендикулярен к касательной плоскости АВ, а радиус С ₂ М' — к касательной плоскости АВ'. По известной теореме геометрии угол между этими перпендикулярами, который мы обозначим y равен углу q между плоскостями:

(88.3)

С другой стороны, угол y, как внешний угол в треугольнике C ₁ NC ₂, равен сумме углов g₁ и g₂, образуемых радиусами R ₁ и R ₂ с осью:

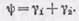(88.4)

Таким образом, с помощью формул (88.2) — (88.4) находим

(88.5)

Мы предположили, что h мала по сравнению с радиу­сами сферических поверхностей R ₁ и R ₂ и с расстоянием f ' точки F' от оптического центра линзы. Поэтому углы g₁, g ₂ и j также малы, и мы можем заменить синусы этих углов самими углами. Далее, благодаря тому, что линза тонкая, мы можем пренебречь ее толщиной, считая C ₁ O=R ₁; C ₂ O=R ₂, а также пренебречь разницей в высоте точек М и М', считая, что они расположены на одной и той же высоте h над осью. Таким образом, мы можем приближенно считать, что

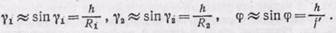(88.6)

Подставляя эти равенства в формулу (88.5), найдем

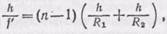(88.7)

или, сокращая на h,

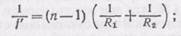(88.8)

отсюда

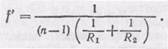(88.9)

Весьма существенно, что h не входит в оконча­тельный результат. Это означает, что любой луч, параллельный главной оптической оси линзы, встре­чающий линзу на любом, но достаточно малом по сравнению с R ₁ и R ₂ расстоянии h от оси, пройдет после пре­ломления в линзе через одну и ту же точку F', лежащую на расстоянии f' от оптического центра линзы.

Таким образом, доказано, что линза имеет главный фокус, и формула (88.9) показывает, как фокусное расстояние зависит от показателя преломления вещества, из которого сделана линза, и от радиусов кри­визны ее преломляющих поверхностей.

Мы предполагали, что параллельный пучок лучей падает на линзу слева направо. Существо дела не изменится, ко­нечно, если на линзу направить такой же пучок лучей, идущих в обратном направлении, т. е. справа налево. Этот пучок лучей, параллельных главной оси, соберется снова в одной точке F — втором фокусе линзы (рис. 196) на расстоянии f от ее оптиче­ского центра. На основании формулы (88.9) заключаем, что f = f ', т. е. оба фокуса лежат симметрично по обе стороны линзы *).

Фокус F называется обычно передним фокусом, фокус F' — задним фоку­сом; соответственно этому расстояние f называется передним фокусным рас­стоянием, расстояние f' — задним фокусным расстоя­нием.

Если в фокусе линзы поместить точечный источник света, то каждый из лучей, выйдя из этой точки и преломив­шись в линзе, пойдет далее параллельно главной оптиче­ской оси линзы, в согласии с законом обратимости световых лучей (см. § 82). Таким образом, из линзы выйдет в этом слу­чае пучок лучей, параллельных главной оси.

При практическом применении полученных нами соот­ношений необходимо всегда помнить о сделанных при вы­воде их упрощающих предположениях. Мы считали, что параллельные лучи падают на линзу на очень малом расстоянии от оси. Это условие не выполняется вполне строго. Поэтому после преломления в линзе точки пересе­чения лучей не будут строго совпадать между собой, а зай­мут некоторый конечный объем. Если мы поставим в этом месте экран, то получим на нем не геометрическую точку,

*) Этот вывод связан с тем обстоятельством, что мы с самого начала полагаем, что по обе стороны линзы находится одна и та же среда (воз­дух). Если бы это было не так, то нарушилась бы и симметрия в располо­жении фокусов F и F',

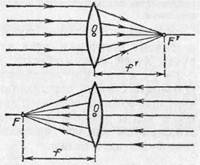
Рис. 196. Фокусы линзы

а всегда более или менее расплывчатое светлое пят­нышко.

Другое обстоятельство, которое нужно помнить, состоит в том, что мы не можем осуществить строго точечный источ­ник света. Поэтому, поместив в фокусе линзы источник хотя бы очень малых, но всегда конечных разме­ров, мы не получим с помощью линзы строго парал­лельный пучок лучей.

В § 70 было указано, что строго параллельный пучок лучей не имеет физического смысла. Сделанное замечание показывает, что рассмотрен­ные свойства линзы находятся в согласии с этим общим физическим по­ложением.

В каждом отдельном случае применения линзы к опре­деленному источнику света для получения параллельного пучка лучей или, наоборот, при применении линзы для фокусировки параллельного пучка надо специально проверять степень отступления от тех упрощающих усло­вий, при которых выведены формулы. Но существен­ные черты явления преломления световых лучей влинзе эти формулы передают правильно, а об отступлениях от них речь будет идти позже.

Date: 2015-05-17; view: 2095; Нарушение авторских прав