Увеличение при изображении объектов в сферических зеркалах и линзах

Увеличение при изображении объектов в сферическом зеркале и линзе. Теперь надо рассмотреть еще вопрос о размерах изображения, получающегося в зеркале и линзе. Выполненные на рис. 210 построения сразу указывают на то, что, в отличие от случая плоского зеркала, размер изображения, даваемого сферическим зер­калом, будет меняться в зависимости от положения объекта по отношению к фокусу зеркала. Так, например, если объект

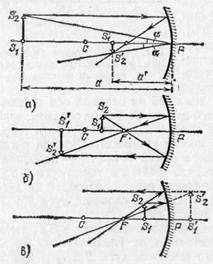
Рис. 210. Изображения про­тяженных объектов в вогну­том сферическом зеркале. Объект расположен: а) за центром зеркала (изображе­ние действительное, обратное и уменьшенное); б) между центром и фокусом (изобра­жение действительное, обрат­ное и увеличенное); в) ближе фокуса (изображение мнимое, прямое и увеличенное)

находится много дальше фокуса вогнутого зеркала, то его изображение получается уменьшенным. Если объект нахо­дится между зеркалом и фокусом, то изображение полу­чается мнимым и увеличенным.

Отношение линейных размеров изображения S ₁ 'S ₂ '=у' к линейным размерам предмета S ₁ S ₂ =y называется линейным, или поперечным, увеличением:

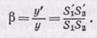
Из подобия треугольников S ₁ PS ₂ и S ₁ 'PS ₂ ' (рис. 210, а) на­ходим

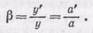(96.1)

Легко убедиться, что равенство (96.1) справедливо и в дру­гих случаях получения изображения при помощи сфериче­ских зеркал (рис. 210, б и в).

Изображения, получаемые с помощью линзы, могут Выть также увеличенными и уменьшенными. Из подобия треугольников S ₁ OS ₂ и S ₁ 'OS ₂ ' (рис. 211) находим для

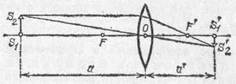
Рис. 211. Линейное увеличение линзы b=S₁'S₂'/S₁S₂=a'/a

увеличения линзы точно такое же выражение, какое мы получили для сферического зеркала:

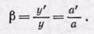(96.2)

Наряду с линейным увеличением мы будем рассматри­вать также угловое увеличение линзы (или сферического зер­кала). Угловым увеличением у называется отношение тан­генсов углов a' и a, составляемых лучом, выходящим из

1.

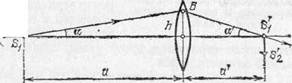
Рис. 212. Угловое увеличение линзы g=tga'/tga=a/a'

линзы, и лучом, падающим на линзу, с оптической осью, т. е.

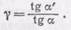(96.3)

Из рис. 212 видно, что

отсюда

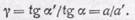
Сравнивая это соотношение с (96.1), находим

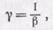(96.4)

т. е. угловое увеличение есть величина, обратная линейному увеличению. Из этого следует, что чем больше линейное

увеличение, т. е. размеры изображения, тем меньше угло­вое увеличение, т. е. тем менее широки пучки световых лучей, образующих изображение. Это обстоятельство имеет важное значение для понимания вопроса о яркости изоб­ражения (см. гл. XI).

Date: 2015-05-17; view: 1184; Нарушение авторских прав