Расстоянии от руки до экрана

Описанные выше явления нару­шения закона прямолинейного рас­пространения света получили на­звание дифракции света.

§ 133. Объяснение дифракции по методу Френеля. Отступления от законов прямолинейного распрос­транения света, примеры которых приведены в предыдущем парагра­фе, получают простое объяснение с точки зрения волновой теории и являются естественным следствием этой теории. Действительно, наб­людаемое в каждом случае распре­деление света есть результат ин­терференции вторичных волн.

Рассмотрим, например, прохож­дение света через круглое отверстие DD в экране (рис. 276). Для того чтобы рассчитать интенсивность света в точке О, применим следую­щий вспомогательный прием. Про­ведем из точки О конические поверх­ности OKL, OMN, OPQ и т. д. до пе­ресечения с поверхностью сферичес­кой волны DCD. Длины образую­щих выберем так, что OL=OC +l/2, ON=OL +l/2 и OQ=ON+ l/2 и

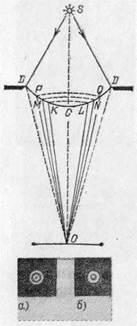
Рис. 276. К объяснению явления дифракции на круглом отверстии. Вни­зу — схематическое изоб­ражение наблюдаемой картины: а) при нечетном числе зон; б) при четном числе зон

т. д. Другими словами, расстояние от точек С, L, N, Q,... до точки О возрастает на длину полуволны (l/2)

*) Приведенные фотографии осуществлены проф. В, К. Аркадье­вым и заимствованы из его статьи.

света, падающего на отверстие. Поверхность волны DCD разобьется на кольцевые зоны. Площади этих зон практиче­ски одинаковы, ибо ОС значительно больше l/2. Но действие их в точке О различно. Действительно, разность хода до точки О между какой-либо точкой первой зоны и соот­ветствующей точкой второй зоны равняется l/2. Поэтому световые волны от первой и второй зон, дойдя до О, будут взаимно ослабляться, так что в точке О действие первой зоны практически уничтожается действием второй зоны. Совер­шенно подобные же рассуждения покажут, что в точке О действие третьей зоны противоположно действию второй, действие четвертой — противоположно действию третьей и т. д, и вообще действия соседних зон практически уничто­жают друг друга. Если отверстие DD таково, что в нем уме­щаются всего две зоны, то в точке О почти не будет света, ибо две соседние зоны взаимно ослабляют друг друга. Большая часть света будет распределена вокруг точки О, так что мы увидим темное пятно, окружен­ное светлым кольцом. При размере отверстия в три зоны в точке О должен быть свет, ибо третья зона ослабит действие второй, и точка будет освещена почти неослаблен­ным действием полной первой зоны» Светлая цен­тральная точка будет охвачена тем­ным кольцом, за которым вновь наблюдается просвет­ление. Вообще при четном числе зон в центре будет темное пятно, окруженное чередующимися светлыми и темными кольцами; при нечетном числе зон — в центре светлее пят­но, а ближайшее кольцо темное и т. д. Размеры этих колец тем меньше, чем больше диаметр отверстия, так что при боль­шом диаметре темные и светлые кольца около центра чере­дуются настолько часто, что мы перестаем различать их и практически не замечаем явлений дифракции.

Аналогичным образом могут быть поняты и другие, бо­лее сложные дифракционные картины. Так как расчет зон Френеля зависит от длины волны света, то, следовательно, и вид дифракционной картины будет зависеть от длины волны. Опыт вполне подтверждает это за­ключение. В частности, в белом свете кольца будут цвет­ными.

§ 134. Разрешающая сила оптических инструментов. Из­ложенное выше показывает, что отверстие, ограничи­вающее проходящую световую волну, обусловливает дифракцию света и приводит к сложной картине распреде­ления освещенных и темных мест. Однако всякий оптический инструмент, в том числе и наш глаз, снабжен линзами или зеркалами, которые всегда ограничивают волновой фронт. Таким образом, следует ожидать, что при полу­чении изображения с помощью оптической системы мы всегда будем иметь дифрак­ционную картину.

Действительно, подробный расчет и опыт показывают, что изображение светящейся точки при помощи объектива представляет собой не просто яркую точку на темном фоне, а довольно сложную систему темных и светлых колец, пе­реходящих друг в друга и по­степенно сливающихся с окру­жающим темным фоном (рис. 277). Чем больше диаметр объектива, дающего изображе­ние, тем мельче эта диф­ракционная картина, т. е. тем теснее располагаются дифракционные кольца. Обычно мы не замечаем этого осложнения и считаем, что изображение светящейся точки есть просто светлая точка. Однако это осложнение всегда имеет ме­сто и при более тщательных наблюдениях может быть обна­ружено. От него нельзя избавиться никаким устройством объектива, ибо оно обусловлено самой волновой при­родой света.

Интересно отметить, что степень дифракционно­го искажения уменьшается по мере увеличения диа­метра объектива (рис. 278); наоборот, искажения, обуслов­ленные погрешностями объектива, например сферической аберрацией, тем больше, чем больше его диаметр (см. § 104).

Рис. 277. Изображение светя­щегося диска (например, планеты), полученное с помощью телескопа (дифракционная картина)

Рис. 278. Уменьшение дифрак­ционных искажений изображе­ний по мере увеличения диа­метра объектива (сверху вниз)

Для фотообъективов обычно погрешности объектива иг­рают большую роль, чем искажения, вносимые дифрак­цией. Поэтому уменьшение диаметра объектива (диафраг­мирование), которое уменьшает роль этих погрешностей, обычно улучшает резкость изображения. Но при доста­точно малых отверстиях искажение вследствие дифракции начнет переве­шивать. Погрешности очень хороших астрономических объективов настоль­ко малы, что основное искажение вносит дифракция, несмотря на то, что эти объективы имеют обычно зна­чительный диаметр (10 см и больше).

Наличие дифракции ставит предел возможности распознавать при помо­щи оптического инструмента дета­ли предмета. Пусть, например, мы рассматриваем в телескоп две звез­ды, расположенные на малом угловом расстоянии друг от друга (рис. 279). В случае совершенного телескопа мы должны были бы, согласно законам геометрической оптики, получить два четких, близко расположенных точеч­ных изображения. Дифракция же при­водит к тому, что вместо двух раздель­ных точек мы получаем картину в виде двух систем светлых и темных колец (рис. 279 снизу).

Если центры этих систем близко расположены (близкие по направле­нию звезды) и кольца не очень мелки (небольшой объектив трубы), то изображения накладывают­ся, давая картину, мало отличающуюся от системы колец, окружающих изображение одиночной звезды. По этой карти­не установить раздельное положение двух звезд становится невозможно: прибор не способен разделить две столь близкие звезды. Итак, способность оптического прибора к различе­нию деталей ограничена волновой природой света. Эту

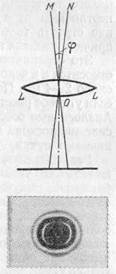
Рис. 279. К понятию разрешающей силы те­лескопа; ОМ, ON— направления на две близкие звезды, j — угловое расстояние между звездами, LL — объектив телескопа. Внизу схематическое негативное изображе­ние

способность объектива принято называть его разрешающей силой. Объективы большего диаметра обладают большей разрешающей силой. Так, телескоп с диаметром объектива 12,5 см может разрешить две звезды, находящиеся на угло­вом расстоянии 1 с", а полуметровый объектив телескопа позволяет различать две звезды, отстоящие на 0,25". Таким образом, в большой телескоп можно иногда рассмотреть от­дельные близкие звезды (звездные скопления), которые для малого телескопа сливаются в общее светящееся пятно и неотличимы от туманностей. Этим объясняется стремле­ние строить телескопы с большими объективами. Другая причина указана в § 119.

Это ограничение в способности распознавания деталей относится и к человеческому глазу, диаметр зрачка которого около 2—4 мм. Поэтому глаз разрешает светящиеся точки, если угловое расстояние между ними около одной минуты *). Аналогичные соображения кладут предел и разрешающей силе микроскопа (§116), где также размер объектива огра­ничивает пучки, участвующие в построении изображения.

Разрешающую силу оптического прибора нельзя сме­шивать с его увеличением (см. § 102). Если увеличенное изо­бражение, полученное при помощи какого-нибудь оптиче­ского прибора, рассматривать при помощи другого оптиче­ского прибора, то увеличение можно сделать сколь угодно большим. Однако это не повысит разрешающую силу си­стемы инструментов. Действительно, изображение, полу­ченное при помощи первого инструмента, будет содержать только такие детали, которые могут появиться при его раз­решающей силе. Дальнейшее увеличение этого изображения, на котором отсутствуют более мелкие детали, конечно, не может их восстановить, а может лишь смазать некоторые де­тали первого изображения; следовательно, разрешающая сила всей совокупности инструментов не может быть боль­ше разрешающей силы худшего из них.

§ 135. Дифракционные решетки. Положение максимумов и минимумов, составляющих дифракционную картину, за­висит, как мы видели, от длины световой волны l. Поэтому при наблюдениях в сложном свете, например в белом, где представлены различные длины волн, дифракционные мак­симумы для различных цветов окажутся на

*) На разрешающую способность глаза, задаваемую диаметром зрач­ка, влияет еще сложная структура сетчатой оболочки глаза. Эта структу­ра ограничивает разрешающую способность глаза угловым расстояни­ем также около 1' (при хорошей освещенности), разных местах, т. е. при явлении дифракции про­исходит разложение сложного света.

Практически наиболее интересный случай дифракции, где такое разложение играет важную роль, осуществляется с помощью так называемых дифракционных решеток.

Простейшая дифракционная решетка представляет собой пластинку, на которой чередуются узкие прозрачные и не­прозрачные полоски, параллельные между собой. Такую решетку можно, например, получить, нацарапав на стекле алмазом ряд штрихов и оставив неповрежденными узкие по­лоски стекла. Очень хорошие решетки получаются также,

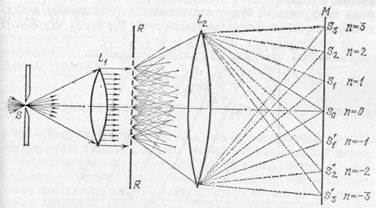
Рис. 280. Действие дифракционной решетки: S — ярко освещенная щель, параллельная штрихам решетки, L₁ — линза, в фокальной пло­скости которой расположена щель, R — дифракционная решетка, L₂ — линза, дающая совместно с L₁ изображение S на экране М, S₀ — изображение щели S с помощью неотклоненных лучей (макси­мум нулевого порядка), S₁, S'₁ — изображения щели S с помощью от­клоненных решеткой лучей (максимумы первого порядка), S₂, S'₂ — изображения щели S с помощью отклоненных решеткой лучей (мак­симумы второго порядка) и т. д.

если нанести царапины на поверхность металлического зер­кала. В этих решетках чередуются полоски, правильно от­ражающие свет, и царапины, разбрасывающие свет во все стороны. Такие решетки называются отражательными. Сумму ширины прозрачной (отражающей) и непрозрачной (рассеивающей) полоски принято называть периодом ре­шетки d. В лучших современных решетках наносят до 1800 штрихов на 1 мм, так что период решетки может быть около 0,8 мкм.

Направим на решетку перпендикулярно к ее поверхности пучок параллельных лучей. Для этого можно ярко осветить узкую щель S, расположенную в фокальной плоскости со­бирающей линзы L ₁ (рис. 280). Свет, проходя через узкие прозрачные полоски решетки RR, испытывает дифракцию, отклоняясь в стороны от своего первоначального направле­ния. При помощи второй линзы L ₂ получим на экране М изображение щели S. Так как вследствие дифракции лучи от решетки падают на линзу L ₂ по разным направ­лениям, то изображения щели S должны расположить­ся в разных местах экрана. Однако благодаря вза­имной интерференции отклоненных пучков некоторые из этих изображений будут отсутствовать (минимумы), а дру­гие будут особенно сильны (максимумы S ₀, S ₁, S' ₁, S ₂, S' ₂...).

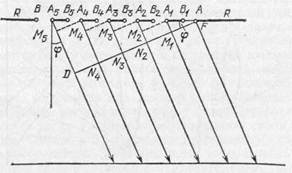
Рис. 281. К теории дифракционной решетки

Результат такой интерференции можно рассчитать, поль­зуясь рис. 281, где изображены несколько рядом располо­женных прозрачных участков решетки. Предположим, что на решетку падает монохроматический свет длины волны l. Пусть фронт падающей волны совпадает с АВ (плоскостью решетки), т. е. свет падает перпендикулярно к решетке. В результате дифракции света на выходе из решетки будут наблюдаться световые волны, распространяющиеся по все­возможным направлениям. Рассмотрим волны, распростра­няющиеся от решетки по направлению, составляющему угол j с нормалью к плоскости решетки. Разности хода лучей, идущих от соответствующих точек отверстий, на­пример от правых краев (точки А, A ₁, A ₂, А ₃,...), от ле­вых краев (точки B ₁, B ₂, B ₃, B ₄...) или от середин отвер­стий и т. д., имеют, конечно, одно и то же значение. Эти разности равны

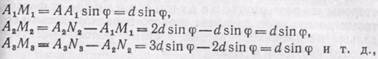
где d=AA ₁ =A ₁ A ₂ =A ₂ A ₃ есть период решетки. Для того чтобы все пучки усиливали друг друга, не­обходимо, чтобы d sinj равнялось целому числу длин волн l, т. е.

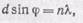(135.1)

где n —целое число. Таким образом, условие (135.1) есть ус­ловие взаимного усиления всех пучков, прошедших через отверстия решетки. Это условие позволяет определить те значения угла j, т. е. те направления, по которым будут наблюдаться максимумы света длины волны l. Эти углы най­дем из формулы

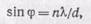(135.2)

давая n различные целые значения: 0, ±1, ±2, ±3 и т. д.

Date: 2015-05-17; view: 629; Нарушение авторских прав