Плоские и сферические зеркала

Изображение точечного источника и протяженного объекта в плоском зеркале. Изображение точечного источ­ника в сферическом зеркале. Мы переходим теперь к задаче нахождения изображений при отражении света от различ­ного типа зеркал. Законы образования изображений светя­щихся точек при отражении в зеркале и при преломлении в линзе во многом аналогичны.

Эта аналогия, конечно, не случайна; она обусловлена тем, что фор­мально, как мы видели в гл. IX, закон отражения является частным случаем закона преломления (при n= —1).

Наиболее просто решается поставленная нами задача для отражения световых лучей от плоского зеркала. Вместе с тем отражение света от плоского зеркала пред­ставляет собой наиболее простой и общеизвестный случай образования мнимых изображений, рассмотренных в пре­дыдущем параграфе.

Пусть пучок лучей от точечного источника S (рис, 203) падает на плоское зеркало (металлическое зеркало, поверх­ность воды и т. д.). Проследим, что произойдет с этим конусом лучей, имеющим вершину в точке S. Возьмем два произвольных луча SA и SB. Каждый из них отра­зится по закону отражения, и угол каждого из них с нор­малью останется после отражения неизменным. Следова­тельно, останется неизменным и угол между лучами по­сле отражения.

Этот угол между отраженными лучами можно изобразить на рисунке, продолжив отраженные лучи назад, за пло­скость зеркала, что показано на чертеже штриховыми ли­ниями. Точка пересечения S ' продолжения лучей за зерка­лом будет лежать на той же нормали к зеркалу, что и точка S, и на том же рас­стоянии от плоскости зер­кала, в чем легко убедиться из равенства треугольников SAO и S'AO или SBO и S'BO.

Ввиду того что рассмотрен­ные лучи SA и SB были со­вершенно произвольными, мы вправе установленные для них результаты отражения от плоского зеркала распростра­нить на весь световой пучок. Следовательно, мы можем утверждать, что при отражении от плоского зеркала пучок световых лучей, исходящих из одной точки, превращается в световой пучок, в котором продолжения всех световых лучей снова пересекаются, в одной и той же точке. В результате наблюдателю, помещенному на пути отраженных лучей, они будут казаться пересекающимися в точке S', и эта точка будет мнимым изображе­нием точки S. Изображение будет мнимым в указан­ном выше смысле: никаких лучей в точке S' за зерка­лом нет, но точка S' является вершиной пучка лучей, повернутого после отражения от зеркала.

Рассмотрение мнимого изображения светящейся точки в плоском зеркале и сделанные выводы о положении этого изображения «за зеркалом» позволяют легко найти также изображение протяженного объекта в плоском зеркале.

Пусть перед зеркалом находится прямолинейный светящийся отрезок АВ (рис. 204, а). Выполняя по найденному рецепту построение точек A ' и В ' и соединяя их прямой, мы получим изображение всех точек отрезка.

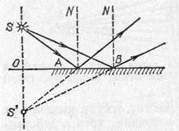
Рис. 203. Образование мнимого изображения точки в плоском зеркале

Это вытекает из элементарных геометрических соображений.

Так как отрезок АВ был выбран совершенно произвольно,

то точно так же можно построить изображение любого

'предмета. При этом из параллельности между собой всех

Рис. 204. а) Образование мнимого изображения прямолинейного отрез­ка в плоском зеркале. 6) Наблюдателю кажется, что свеча горит в бутылке с водой, расположенной за стеклянной пластинкой там, где на­ходится мнимое изображение свечи в этой пластинке

нормалей к зеркалу ясно, что размеры мнимого изображе­ния в плоском зеркале равны размерам предмета, постав­ленного перед зеркалом.

В решении, найденном для случая отражения световых пучков от плоского зеркала, необходимо подчеркнуть, что каждая точка све­тящегося объекта изобразится в плоском зеркале также в виде точки (т. е. стигматически).

Переходим теперь к рас­смотрению сферических зеркал. На рис. 205 изображено сечение AРВ вогнутого сферического зеркала радиуса R; С — центр сферы. Средняя точка имеющейся части сферичес­кой поверхности называет­ся полюсом зеркала Р. Нормаль к зеркалу, проходящая через центр зеркала и через его полюс, называется главной типической осью зеркала. Нормали к зеркалу, проведенные в других точках его поверхности и также, конечно, проходя­щие через центр зеркала С, носят название побочных оптических осей. Одна из них (МС) показана на рис. 205. Все

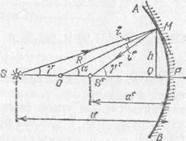
Рис. 205. Отражение от сферичес­кого зеркала луча SM, выходяще­го из точки S на оси

нормали к сферической поверхности, конечно, равноправ­ны, и выделение главной оптической оси среди побочных не является существенным *). Диаметр окружности, ограни­чивающей сферическое зеркало, носит название отверстия зеркала.

Все дальнейшее есть упрощенное повторение сказанного в §§ 88, 89 относительно линз.

Пусть точечный источник света S расположен на главной оси зеркала на расстоянии SP=a от полюса. Так же, как и в случае линз, рассмотрим луч SM, принадлежащий к узкому пучку, т. е. образующий с осью малый угол у и падающий на зеркало в точке М на высоте h над осью, так что h мало по сравнению с а и с радиусом зеркала R. Отраженный луч пересечет ось в точке S' на расстоянии S'Р=а' от полюса. Угол, образуемый отраженным лучом с осью, обозначим g '. Он также будет мал.

Очевидно, СМ есть перпендикуляр к поверхности зер­кала в точке падения, i — угол падения, i' — угол отраже­ния. По закону отражения

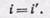(91.1)

Обозначим буквой a угол, образуемый радиусом СМ с осью. Из треугольника SMC имеем

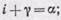(91.2)

из треугольника CMS'

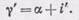(91.3)

Складывая (91.2) и (91.3) и учитывая, что i=i ', находим

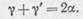(91.4)

Так как мы рассматриваем узкий пучок лучей, прилега­ющих к главной оси, т. е. углы g, g' и a малы, то мы можем заменить синусы углов самими углами и пренебречь дли­ной отрезка PQ. Тогда мы будем иметь приближенные ра­венства:

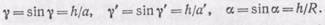(91.5)

Подставляя полученные равенства в уравнение (91.4) и со­кращая на общий множитель h, находим

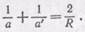(91.6)

*) В линзах главная оптическая ось существенно отличается от по­бочных тем, что она есть единственная ось, проходящая через центры обеих сферических поверхностей, ограничивающих линзу.

То, что высота h, равно как и угол g, не входят в окончательный результат, означает, что любой луч, выходящий из точки S (и принадлежащий к достаточно уз­кому пучку), после отражения пройдет через точку S' на расстоянии а' от полюса. Таким образом, точка S ' есть изображение точки S.

Мы видим, что при отражении в сферическом зеркале изображением точечного источника является снова точка. Как и в случае линзы, точка S, в которой расположен ис­точник, и точка S', в которой находится изображение, сопряжены между собой, т. е., поместив источник в точку S', мы получим изображение в точке S (следствие закона обратимости световых лучей, см. § 82).

Полученная нами формула (91.6) является основ­ной формулой сферического зеркала.

Легко доказать, что для выпуклого сферического зер­кала формула (91.6) остается в силе.

Date: 2015-05-17; view: 1321; Нарушение авторских прав