Уравнение баланса внутренней энергии

Удельная внутренняя энергия 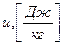определяется с точностью до постоянной 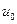и линейно зависит от температуры . для капельных жидкостей 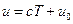, для калорически совершенных газов 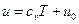, где 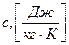– удельная теплоемкость жидкости, 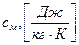– удельная изохорная теплоемкость газа.

Уравнение баланса внутренней энергии в интегральной форме может быть получено вычитанием уравнения (3.23) из (3.30).

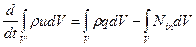(3.37)

или, полагая, , с учетом (3.31) и (3.28)

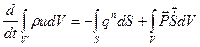(3.38)

Для преобразования уравнения (3.38) в алгебраическую форму для контрольных объемов 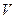, запишем правую часть (3.38) в виде:

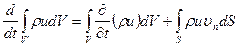(3.39)

Тогда из (3.38) и (3.39) получим:

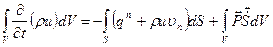(3.40)

Область течения разбиваем на конечное число малых, но конечных контрольных объемов (КО) – 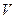. В пределах каждого КО полагаем линейным или экспоненциальным изменение параметров по пространственным координатам и времени (см. п.4.4.).

Тогда из (3.40) получим уравнение баланса внутренней энергии в алгебраической форме.

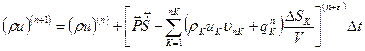, (3.41)

где – число граней контрольного объема, 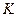– номер грани.

Для получения дифференциального уравнения баланса внутренней энергии преобразуем левую часть (3.37), с использованием закона сохранения массы.

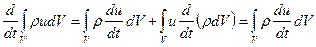(3.42)

Поверхностный интеграл в (3.38) преобразуем в объемный по формуле Остроградского-Гаусса

.

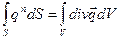Тогда из (3.37) и (3.31) получим:

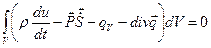(3.43)

Ввиду произвольности 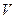подынтегральная функция в (3.43) равна нулю:

. (3.43)

Используя закон Фурье для теплового потока из-за теплопроводности 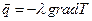, где 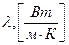– коэффициент теплопроводности, получим уравнение:

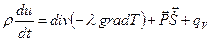(3.44)

Учитывая выражения для

; ,

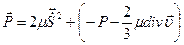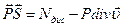где 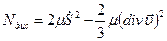– диссинируемая мощность, т.е. необратимая часть мощности внутренних сил с противоположным знаком.

Тогда уравнение баланса внутренней энергии запишется в виде:

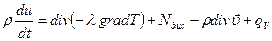(3.45)

откуда следует, что изменение внутренней энергии происходит за счет подвода тепла вследствие теплопроводности, работы сил трения при деформации частиц, работы при деформации за счет сил давления и выделения теплоты за счет источников в потоке.

Уравнение баланса внутренней энергии 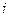-ой фазы аналогично (3.37), но включает в себя слагаемое, определяемое энергетическим взаимодействием между 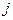-ыми и 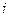-ой фазами .

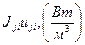Аналогично (3.43) выводится уравнение баланса внутренней энергии 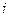-ой фазы в дифференциальной форме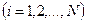

,

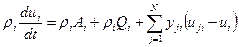где 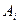и 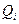представляют собой работу внутренних сил и притока тепла в единицу времени, отнесенные к единице массы 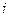-ой фазы.

Date: 2015-05-09; view: 802; Нарушение авторских прав