Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Уравнение движения в интегральной форме
|
|
В механике сплошных сред теорема об изменении главного вектора количества движения однофазной среды формулируется следующим образом: индивидуальная производная от главного вектора количества движения «жидкого объема» равна сумме главных векторов внешних объемных поверхностных сил, приложенных к частицам, расположенным соответственно в объеме и на поверхности:
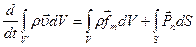(1)
Для многофазного континуума, состоящего из N фаз, уравнение движения записывается для каждой из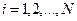 
фаз. В правой части уравнения (1) добавляется главный вектор сил, связанных с межфазным взаимодействием.
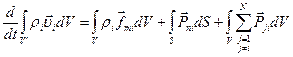, (2)
где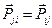 
– интенсивность обмена импульсом между j -й и i -ой составляющими (фазами).
Уравнения (1) и (2) выражают закон об изменении количества движения. Они относятся к основным законам природы для сплошных сред и подтверждены огромным количеством опытных данных.
Date: 2015-05-09; view: 614; Нарушение авторских прав