Уравнение неразрывности для многофазной среды

Выделим в пространстве фиксированный контрольный объем 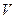. Уравнение баланса массы записывается для каждой 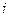-ой фазы многофазной среды в объеме :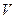

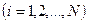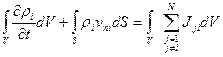, (1)

где первое слагаемое представляет собой массу 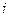-ой фазы, накапливающуюся в объеме 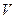за единицу времени 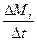; второе слагаемое – расход 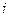-ой фазы через поверхность 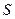, ограничивающую объем 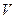, 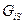; в правой части уравнения (2.26)1 – масса 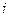-ой фазы, образующейся в объеме 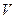за единицу времени вследствие перехода массы из всех 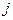-ых фаз 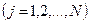вследствие фазовых переходов и химических реакций;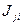 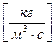– интенсивность перехода массы из 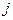-ой фазы в 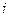-ую составляющую ,

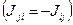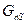
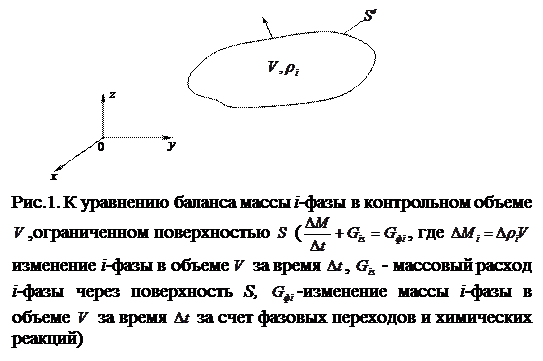
Для записи (1) в алгебраической форме область течения разбиваем на малые контрольные объемы 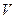. Производная от плотности 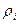по времени для каждого малого объема записывается через конечные разности:

,

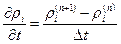где верхние индексы 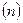и 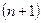соответствуют параметрам в моменты времен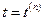и и 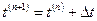. Интегралы в уравнении (12.26) заменяются их приближенными выражениями по «теореме о среднем». Тогда получаем уравнение неразрывности для 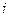-ой фазы в алгебраической форме:

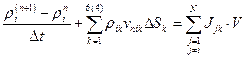(2)

где верхний параметр 6 соответствует шести граням в 3D-пространстве, 4 –четырем граням контрольного объема на плоскости.

Для записи (1) в дифференциальной форме используется формула Гаусса-Остроградского:

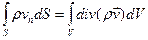
Тогда для объема 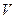в области непрерывного движения имеем:

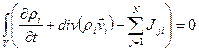
откуда, вследствие произвольности объема 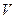получаем уравнение неразрывности в дифференциальной форме:

(3)

Если просуммировать равенство (3) по 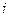с учетом 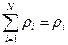(где 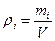– приведенная плотность фаз, 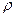– плотность смеси) и 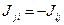получим уравнение неразрывности смеси в целом или для однофазной среды

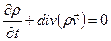(4)

Для установившегося движения 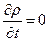и уравнении неразрывности для сжимаемой жидкости в декартовой системе координат имеет вид:

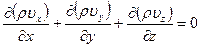(5)

Для установившегося двумерного течения несжимаемой жидкости уравнение неразрывности упрощается

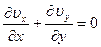(6)

Для установившегося движения сжимаемой среды в струйке тока или в канале (рис. 2.), из (1) при 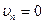на поверхности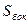

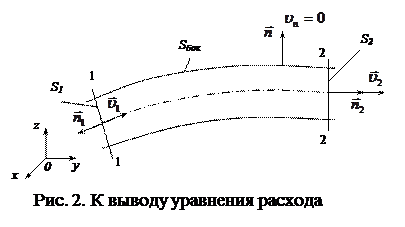
К выводу уравнения расхода

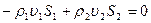, (7)

откуда

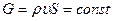
вдоль струйки тока или в канале, где 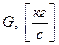– массовый расход.

Date: 2015-05-09; view: 1196; Нарушение авторских прав