Уравнения турбулентного движения в форме Рейнольдса

Рассмотрим уравнение неразрывности для мгновенных значений скорости и плотности при неустановившемся движении сжимаемой среды.

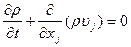(11.26)

Где производится суммирование по повторяющимся индексам

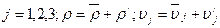(11.27)

Для несжимаемой жидкости (ρ=сonst) уравнение неразрывности превращается:

(11.28)

Проведем осреднение слагаемых (11.28) по правилу (11.2)

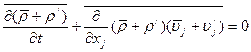
Тогда, с использованием свойств осреднения 1(11.4), 5(11.8), 8(11.11), 4(11.7), 9(11.12), получим

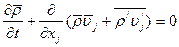(11.29)

Введем обозначение . Тогда уравнение неразрывности примет вид, совпадающий по форме с (11.26)

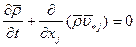(11.30)

Для несжимаемой жидкости 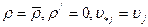уравнение (11.30) упрощается

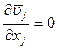(суммирование по j=1,2,3) (11.31)

В системе координат (x,y,z) уравнение неразрывности при турбулентном течении несжимаемой среды имеет вид

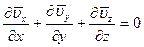
Вычитая (11.31) из (11.28) получим уравнение неразрывности для мгновенных пульсационных значений скорости

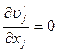(11.32)

Уравнение движения Навье-Стокса запишем для мгновенных значений скорости, плотности, давления, массовой силы и коэффициента вязкости в проекции на оси x_i (i =1,2,3)

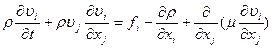(11.33)

Умножим уравнение (11.31) на 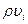. Получим уравнение

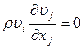(11.34)

Сложим уравнения (11.33) и (11.34)

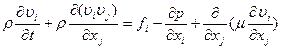(11.35)

Осредним уравнение (11.35) по правилу (11.2)

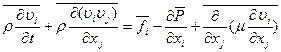(11.36)

Положим для простоты дальнейших выкладок 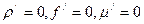. Тогда используя свойства 1,5,8,4 и 9 осреднения (11.2) получим

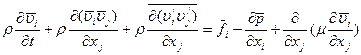(11.37)

Разделив (11.37) на плотность ρ и обозначив снова 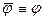, то есть отбросив формально знаки осреднения, получим уравнение Рейнольдса для осредненного турбулентного течения в проекции на оси координат

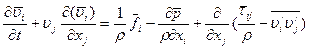(11.38)

Уравнение (11.38) называется уравнением Рейнольдса. Это уравнение содержит новые неизвестные корреляции скорости . Величины 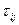представляют собой напряжения, которые возникают при ламинарном движении среды, добавочные напряжения возникающие в турбулентном потоке можно записать как 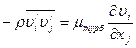, где 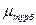- динамический коэффициент турбулентной вязкости. Добавочными напряжениями в турбулентном потоке называются напряжения Рейнольдса. Напряжения Рейнольдса образуют симметричный тензор второго ранга - тензор “турбулентных напряжений”

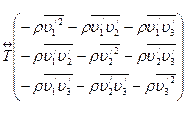(11.39)

Компоненты тензора турбулентных напряжений характеризуют перенос осредненного количества пульсационного движения (импульса) пульсационными скоростями. Тензор напряжений в турбулентном потоке с учетом “турбулентных” напряжений можно представить в виде

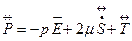(11.39)

где компоненты тензора 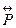выражаются как

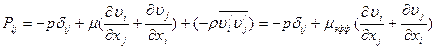, (11.40)

где - эффективный коэффициент вязкости.

Date: 2015-05-09; view: 1014; Нарушение авторских прав