Квазистационарный метод Л.С. Лейбензона для приближенного решения задач Стефана. Задача о промерзании цилиндрической трубы

Для задач Стефана лишь в редких простейших случаях удается найти точ­ное ана­ли­ти­чес­кое решение, поэтому приходится применять приближенные ме­то­ды. Один из наиболее рас­про­стра­ненных в инженерной практике методов, по­зволяющий получить решения ряда прак­ти­чески важных задач, был пред­ло­жен в 1931г. Л.С.Лейбензоном. Идея этого метода за­клю­ча­ет­ся в замене ре­аль­но­­го распределения температуры распределением, удов­лет­во­ря­ю­щим урав­не­нию Лапла­са (по этой причине данный метод иногда называют ква­зи­ста­ци­о­нар­ным), а пос­ле нахождения температурного поля скорость движения фронта оп­­ре­де­ля­ется с помощью ус­ло­вия Стефана. Метод Лейбензона применим в тех слу­чаях, когда ско­рость установления тем­пе­ратуры много больше, чем скорость дви­жения фронта фазового пе­ре­хода v. Если x - ха­рак­тер­ный размер задачи, то x²/a - характерное время установления температуры. Если за это вре­мя фронт фа­зового перехода проходит расстояние, много меньшее, чем x, то реальное рас­­пре­деление температуры можно заменить установившимся, т.е. условие при­менимости ква­зи­ста­ционарного метода можно записать в виде:

vx²/a << x, или a >> vx. (1)

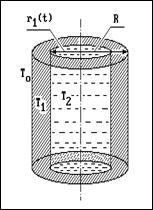
Рассмотрим в качестве примера очень важную с практической точ­ки зре­ния задачу о про­мерзании трубопровода, заполненного жид­костью. Пусть име­ется неограниченный по вы­­соте цилиндр (тру­ба) радиуса R, заполненный жид­костью при температуре Т₂ = Т_ф = 0. В не­который мо­мент вре­мени на по­вер­хности цилиндра скачком ус­та­нав­ли­вается, а затем под­дер­живается по­­сто­ян­­ной температура Т_о < Т_ф. Фронт промерзания начинает двигаться от по­верх­нос­ти к оси ци­лин­д­ра, и через некоторое время вся жидкость в трубе замерзает. Обо­­зна­чим через T₁ температуру льда в промерзшей зоне, через r₁ - ко­ор­ди­на­ту фронта про­мер­за­ния. Требуется найти закон движения фрон­та про­мер­за­ния r₁(t) и время пол­но­го промерзания t. Температура льда в промерзшей зоне опре­де­ля­ется уравнением теплопроводности:

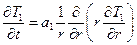, r₁(t) £ r £ R, (2)

с граничными условиями

T₁(R,t) = T₀, T₁(r₁,t) = T_ф = 0. (3)

Т.к. температура жидкости считается всюду постоянной и рав­ной T_ф, то градиент тем­пе­ра­ту­ры, а вместе с ним и теп­ло­вой поток в жидкости равны нулю, поэтому условие Сте­фа­на при­ни­ма­ет вид:

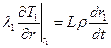. (4)

Будем решать задачу квазистационарным методом Лей­бен­зо­на. Положим в уравнении (2) ¶T₁ /¶t = 0, тогда ста­ционарная температура в области r₁ £ r £ R будет равна:

T₁ = C₁lnr +C₂,

а константы интегрирования C₁ и C₂ определяются из граничных ус­ло­вий (3):

, .

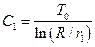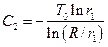Таким образом, стационарное распределение температуры в промерзшей об­лас­ти имеет вид:

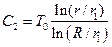, и .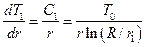

Подставляя последнее равенство в условие Стефана (4), получаем диф­фе­рен­циальное уравнение относительно координаты фронта r₁:

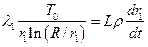
с разделяющимися переменными:

.

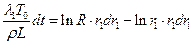В результате интегрирования (второй интеграл справа берется по частям), на­хо­дим:

.

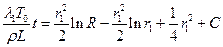Константу интегрирования C найдем из начального условия: r₁ = R при t = 0:

.

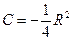Таким образом, получаем формулу, выражающую взаимно-однозначное со­от­вет­ствие между r₁ и t:

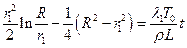, (5)

которую и можно считать законом движения фронта промерзания (выразить в явном виде фун­к­цию r₁(t) не удается, но это несущественно). Время полного промерзания t найдем из ус­ло­вия r₁ = 0:

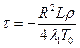, (6)

где знак "минус" означает, что полученное решение имеет смысл, если T₀ < 0.

Проверим применимость полученного решения для конкретного примера - про­мерзания во­ды в трубопроводе. Характерным размером в данном случае яв­ляется радиус трубы R, а средняя скорость движения фронта промерзания рав­на v» R/t. Подставляя эти значения в условие при­ме­нимости метода Лей­бен­зона (1), находим:

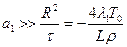, или .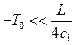

Удельная теплота фазового перехода вода-лед L» 335 кДж/кг, удельная теп­ло­ем­кость льда c₁» 2.1 кДж/(кг×К), поэтому полученное решение применимо для не слишком низких температур на поверхности трубопровода: - T₀ << 40⁰C.

Date: 2015-05-09; view: 1639; Нарушение авторских прав