Нестационарное одномерное температурное поле в полуограниченной среде с заданной постоянной температурой на поверхности

1.Изменение температуры в неограниченной среде. Пусть в неограни­чен­ной среде задано начальное распределение температуры T = f(x). Для того, чтобы определить, как это распределение будет изменяться со временем, можно каж­дую точ­ку среды считать источником с количеством тепла, равным:

q = rcTdx' = rcf(x')dx'.

Тогда температуру в любой точке среды в любой момент времени можно за­пи­сать в виде ин­те­гра­ла от фундаментального решения по x', полагая в этой формуле t' = 0:

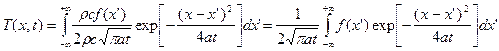. (1)

Формула (1) дает решение поставленной задачи, если задан конкретный вид функции f(x).

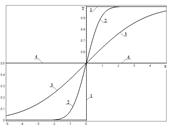Рассмотрим пример, имеющий важное практическое значение. Пусть два одинаковых тела прямоугольной формы на­греты до раз­лич­ных тем­пе­ратур. Примем за нуль начальную тем­пе­ратуру более холодного тела, а начальную тем­пе­ра­ту­ру более на­гре­того тела обо­зна­чим через T₁. Пусть в момент времени t' = 0 эти те­ла при­ве­де­ны в со­прикосновение (см. рисунок), так что получается одно не­рав­но­мер­но нагретое тело, и пусть размер этого тела до­ста­точно велик, так что мож­но применить формулу (1). То­гда на­чаль­ное распределение температуры (функция f(x')) бу­дет иметь вид "ступеньки": нуль при x' < 0 и T₁ при x' > 0 (ли­ния 1 на ри­сун­ке), и фор­му­ла (1) при­ни­ма­ет вид:

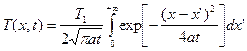. (2)

Вычислить этот интеграл удобно по отдельности для об­лас­тей x > 0 и x < 0. В области x > 0 сде­лаем замену: (x-x')²/(4at) = a². Тогда 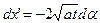, пределы интегрирования: x' = 0 ® 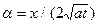, x' = ¥ ® a = -¥, и фор­мула (2) принимает вид:

=

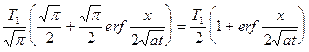= , x > 0.

В области x < 0 обозначим: x = -| x | и сделаем замену: ( -| x | -x')²/(4at) = ( | x |+ x')²/(4at) = a². Тогда 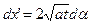, пределы интегрирования: x' = 0 ® 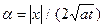, x' = ¥ ® a = ¥, и фор­мула при­нимает вид:

=

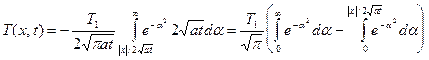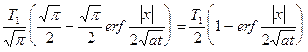= , x < 0.

Итак, вычисление интеграла (2) приводит к следующему результату:

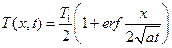, x > 0. (3)

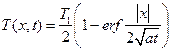, x < 0. (4)

На рисунке изображен вид кривых T(x) в различные моменты времени t₁ и t₂ > t₁ (кри­вые 2 и 3). Тепло постепенно перетекает из более нагретой области в более хо­лодную. В пре­деле при t ® ¥, как видно из формул (3) и (4), во всей сре­­де установится одинаковая тем­пература T = T₁ /2 (линия 4), как и должно быть по закону сохранения энергии. В точке x = 0 (в плоскости со­при­кос­но­ве­ния тел) температура равна T₁ /2 в любой момент времени, как и долж­но быть из соображений симметрии.

2. Нестационарное одномерное температурное поле в полуограниченной сре­де с за­дан­ной постоянной температурой на поверхности.

Рассмотрим теперь полуограниченную среду, на по­верх­ности которой поддерживается по­стоянная температура T₁. Ре­шим сначала задачу для частного случая T₁ = 0, а затем обоб­щим полученный результат на ненулевую тем­пературу.

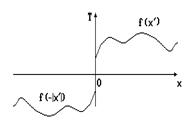
Пусть среда занимает область x > 0 и имеет некоторое про­из­вольное начальное рас­пре­деление температуры T = f(x). Вос­поль­зуемся предыдущим ре­зуль­татом, для чего продолжим (мыс­лен­но) среду в область x < 0, при­чем будем считать, что в этой об­ласти

f (-| x' |) = -f(x') (5)

(см. ри­су­нок). Тогда температурное влияние каж­дой точки из об­лас­ти x > 0 на границу x = 0 будет ком­пен­си­ро­ваться влиянием сим­метричной точки из области x < 0, и гра­ничное условие

T(0,t) = T₁ = 0

будет, очевидно, удовлетворено автоматически, а распределение температуры в любой в точке x > 0 в любой момент времени можно записать в виде:

.

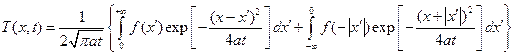Учтем во втором интеграле условие (15.5) и одновременно поменяем пределы этого ин­те­гра­ла:

.

Эта формула определяет температуру в любой точке x полуограниченной среды в любой мо­мент времени t, если задана начальная температура среды f(x'), а на поверхности x = 0 под­дер­жи­вается нулевая температура.

Если f(x') = const = T₀, то эту величину можно вынести из-под знака интеграла. Тогда, вы­пол­няя вычисления аналогично тому, как это было сделано при выводе формул (3) и (4), на­ходим:

=

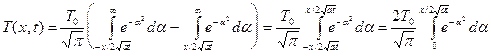= . (6)

Формула (6) определяет температуру в любой точке x полуограниченной среды в любой момент времени t, если начальная температура среды была T₀ = const, а на поверхности x = 0 поддерживается нулевая температура T₁ = 0.

Обобщить полученный результат на ненулевую температуру на поверхности T₁ ¹ 0 проще всего переходом к новой переменной T' = T - T₁. Тогда T'₀ = (T₀ - T₁), и

,

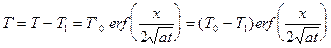отсюда

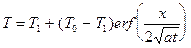. (7)

Формула (7) определяет температуру в любой точке x полуограниченной среды в любой момент времени t > 0, если начальная температура среды была T₀ = const, а на поверхности x = 0 начиная с момента времени t = 0 поддерживается постоянная температура T₁.

Если T₀ = 0, то

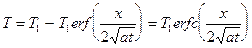. (8)

Date: 2015-05-09; view: 964; Нарушение авторских прав