Температурное поле непрерывного плоского источника. Нагрев полуограниченной среды постоянным потоком тепла

1.Температурное поле мгновенного плоского источника. Пусть в каж­дой точке (точнее, на каждом участке с размерами dy'×dz') некоторой плос­кос­ти x' = const в момент времени t' мгновенно вы­де­­лилось количество тепла, равное q×dy'×dz'. Пред­ста­вим эту плоскость источником тепла, име­ю­щим бес­ко­неч­ные размеры в y - и z -на­прав­ле­ниях, и проинтегрируем фундаментальное решение по y' и z' от -¥ до +¥:

=

= .

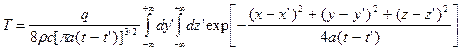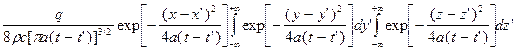Сделаем в интеграле по z' замену переменных: (z-z')²/[4a(t-t')] = a². Тогда 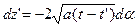, и интеграл преобразуется в интеграл Пуассона, умноженный на 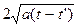. Совершенно ана­ло­­гично преобразуется интеграл по y'. Таким образом, интегри­ро­вание по y' и z' дает мно­жи­тель 4a(t-t')p, и в результате получаем:

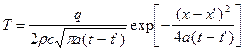. (1)

Формула (1) определяет одномерное температурное поле, создаваемое мгно­венным плос­ким источником тепла в неограниченной среде, т.е. температуру точки среды с координатой x в любой момент вре­мени t > t', если в плоскости с ко­ординатой x' момент времени t' мгновенно выделилось количество тепла, рав­ное q (на еди­ни­цу площади).

2.Температурное поле непрерывного плоского источника. Пусть в плос­кости x' = const в момент времени t' = 0 начинает непрерывно действовать плос­кий источник тепла с мощностью W на единицу площади. Выберем для крат­кос­ти записи x' = 0, т.е. поместим начало координат в плоскость, где находится ис­точник. За время dt' этот источник выделяет количество тепла, равное q = Wdt' (на единицу площади). Для нахождения температурного поля, соз­да­вае­мо­го этим источником, проинтегрируем формулу (1) по t' от 0 до t:

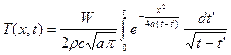. (2)

Сделаем замену переменных: x²/[4a(t - t')] = a². Тогда: (t - t')^1/2 = x/(2a^1/2a), dt' = x²da/(2aa³), пределы интегрирования: t' = 0 ® 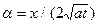, t' = t ® a = ¥, и фор­мула принимает вид:

.

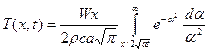Учтем, что rca = l. Интегрируем по частям. Обозначим: 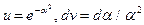. Тогда 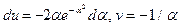, и получаем:

.

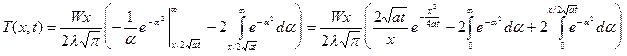Первый интеграл в скобках справа - это интеграл Пуассона. Раскрывая скобки, находим:

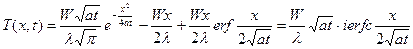. (3)

Эта формула определяет температурное поле непрерывного плоского ис­точ­ни­ка в не­о­гра­ни­чен­ной среде.

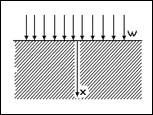
3.Нагрев полу­ограни­чен­ной среды постоянным по­то­ком тепла. Рассмотрим теперь полуограниченную среду (это может быть большой участок грунта с ровной по­верх­ностью, стена большой тол­щи­ны, толстая пластина и т.п.), нагреваемую по­сто­ян­ным тепловым по­­то­ком с плот­ностью мощности W = const (см. ри­су­нок). Считая каж­дую точку нагреваемой по­верх­ности источ­ни­ком теп­ла, мы мо­жем применить полученный результат для оп­ре­де­ле­­ния тем­пе­ра­тур­но­го поля в этой среде. Надо лишь учесть, что, в от­ли­чие от не­о­гра­ни­ченной среды, теп­ло будет рас­про­стра­няться толь­ко в на­прав­ле­нии x > 0, поэтому "эффективность" нагрева бу­дет в два ра­за выше, чем ес­ли бы тепло распространялось в обе стороны, сле­до­вательно, фор­му­ла, оп­ре­де­ля­ющая тем­пе­ра­турное поле в полу­огра­ни­ченной среде, отличается от формулы (3) мно­жи­те­лем 2:

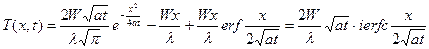. (4)

Date: 2015-05-09; view: 786; Нарушение авторских прав