Основное уравнение молекулярно-кинетической теории. Как следует из названия раздела, здесь мы отойдем на время от термодинамического метода и обратим внимание на статистический подход

Как следует из названия раздела, здесь мы отойдем на время от термодинамического метода и обратим внимание на статистический подход. Задача данного раздела - количественно объяснить давление газа на стенки сосуда как результат совместного действия молекул, составляющих газ. Вы также убедитесь на примере газа, что термодинамический и статистический подходы действительно дополняют друг друга, давая новую информацию. В частности, будет найдена связь средней кинетической энергии молекул газа с температурой.

Физическая модель идеального газа. В разделе 1 был оценен характерный размер d молекулы (на примере воды), который оказался равным 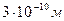. Там же говорилось, что несжимаемость воды, по-видимому, связана с тем, что молекулы практически касаются друг друга, то есть размер d сравним с расстоянием между центрами молекул. В газах это, по-видимому, не так, поскольку объем может сильно уменьшаться.

Оценим среднее расстояние 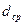между молекулами газа при нормальных условиях. Согласно закону Авогадро 1 моль любого газа при нормальных условиях занимает объем 22,4 10 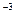м 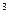/моль. Значит, на одну молекулу приходится объем в Na раз меньший:

.

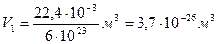Поскольку V₁ @ 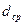, получим:

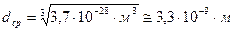
Таким образом, в газе среднее расстояние между молекулами на порядок больше характерного размера молекул: d _ср/ d @ 10. Это обстоятельство позволяет принять следующую модель идеального газа:

1) Газ сильно разрежен, так что собственный объем молекул газа V _мол@ N _а m/m V₁ существенно меньше объема сосуда, в котором находится газ (V_{мол. <} V).

2) Силами взаимодействия между молекулами такого разреженного газа можно пренебречь и учитывать взаимодействие только при столкновении молекул.

3) Столкновения молекул газа между собой и со стенками сосуда являются абсолютно упругими (молекулы - упругие шарики).

4) Молекулы газа совершают беспорядочное тепловое движение, т.е. направления скоростей ориентированы в пространстве совершенно беспорядочно. Это означает, что в каждом направлении в данный момент движется одинаковое число молекул, т.е. N/6, где N - полное число молекул газа (N/3 молекул движется параллельно каждой из осей координат, причем половина из них движется в положительном направлении, а другая - в противоположную сторону).

Давление молекул на стенку сосуда. Давление согласно определению равно силе, с которой газ воздействует на площадку единичной площади, перпендикулярно площадке:

,

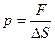где DS - площадь плоской площадки, например стенки сосуда.

Величина суммарной силы воздействия молекул на площадку по III закону Ньютона равна суммарной силе, действующей на систему молекул со стороны площадки. Следовательно, сила может быть найдена по II закону Ньютона для системы материальных точек:

,

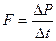где P - суммарное изменение импульса всех молекул, сталкивающихся за время Dt с площадкой DS.

Для того, чтобы вычислить DP, необходимо, во-первых, знать число молекул N', которые ударяются о площадку за малое время Dt, и, во-вторых, изменение импульса каждой молекулы.

Если молекула массы m ₀ налетает в направлении, перпендикулярном площадке, со скоростью u, то в результате абсолютно упругого удара с тяжелой площадкой (масса сосуда много больше массы молекулы) молекула отскочит с такой же скоростью в противоположном направлении (это известно из механики). То есть изменение импульса одной молекулы равно:

.

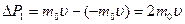Теперь необходимо вычислить число молекул N'. Сколько молекул столкнутся с площадкой за время Dt? Это будут все молекулы, расположенные в объеме DV и летящие в направлении, перпендикулярном площадке. Значит, это составит 1/6 от всех молекул, содержащихся в объеме DV:

,

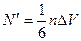где n - концентрация молекул газа, т.е. число молекул в единице объема.

Чем определяется объем DV? Это тот объем, из которого молекулы, движущиеся в сторону площадки, успевают ее достичь за время Dt (см. рис.1.6). Значит, высота равна uDt, а основание - DS, что позволяет определить DV=DS uDt и записать выражение для числа столкновений:

.

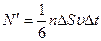uDt

DS

Рис. 1.6. Объем DV, из которого молекулы достигают площадки за время Dt

Поэтому DP=2m₀ut N'= 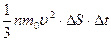и окончательно получим:

.

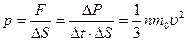Таким образом, мы получили формулу:

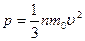. (1.12)

Используя понятие средней кинетической энергии теплового движения молекул 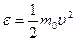, уравнение (1.12) можно записать в виде:

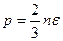. (1.13)

Это есть основное уравнение молекулярно-кинетической теории идеального газа,} которое означает:

Date: 2015-05-09; view: 709; Нарушение авторских прав