Масса и размеры молекул

Для того, чтобы измерить какую-либо величину, нужно сравнить ее с другой величиной, которая принята за эталон (или за единицу измерения). Поскольку массы молекул очень малы, для их измерения удобно взять также малую единицу измерения. За единицу измерения масс в молекулярной физике принимают одну двенадцатую (1/12) часть атома 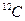(так обозначается изотоп углерода с массовым числом 12). Эта масса называется атомной единицей массы.

Массы различных молекул принято характеризовать относительной молекулярной массой вещества 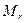, которая равна отношению массы молекулы данного вещества m к атомной единице массы: 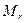= m / . Для краткости эту величину часто называют молекулярной массой, однако следует помнить, что эта величина является безразмерной величиной, а, зная ее, массу молекулы данного вещества можно вычислить согласно формуле .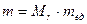

Далее для описания количества вещества часто будет использоваться понятие - моль. Молем называется количество какого-либо вещества, в котором содержится столько же молекул, сколько их в 0,012 кг изотопа углерода .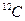

Очевидно, что моли всех веществ содержат одно и то же число молекул, которое принято обозначать 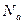. Величина 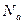является фундаментальной величиной и называется числом Авогадро. Опытным путем удалось найти, что число Авогадро равно:

.

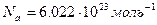Таким образом, можно сказать, что моль - это такое количество вещества, в котором содержится число Авогадро молекул.

Массу одного моля вещества называют молярной массой и обозначают буквой 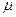. Нетрудно сообразить, что для того, чтобы найти молярную массу, нужно массу одной молекулы умножить на число Авогадро:

.

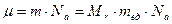Эта формула справедлива для любых веществ, в том числе и для углерода 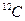, в случае которого молярная масса, как сказано ранее, равна 0,012кг. В случае углерода 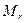=12, что очевидно. В результате, все величины, входящие в последнюю формулу, кроме являются известными. Поэтому эту формулу, записанную для углерода, можно использовать для определения величины :

.

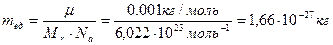Из последней формулы следует, что произведение двух констант 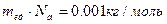. Подставляя это значение в формулу (1.1), получим:

.

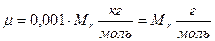Таким образом, мы пришли к важному выводу, что масса моля, выраженная в граммах, численно равна относительной молекулярной массе. Однако следует иметь в виду, что в то время, как 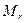- величина безразмерная, 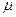имеет размерность кг/моль (или г/моль).

Вывод: на практике нет необходимости вычислять молярную массу по формуле (1.1) - достаточно взять относительную молярную массу и умножить на 0,001. Результат получим в кг/моль.

Пример решения задач

Задача 1

Вычислить молярную массу воды. Сколько молекул N воды содержится в чашке чая, объемом V=180 .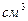

Химическая формула воды - 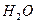. Далее находим (например, в периодической таблице Менделеева), что относительная атомарная масса водорода равна 1, а кислорода - 16. Поэтому относительная молярная масса молекулы воды 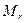=2 1+16=18 (молекула содержит два атома водорода). Используя только что сформулированное правило, придем к выводу, что 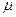=18г/моль=0,018кг/моль.

Ответить на второй вопрос можно, вычислив число молей воды в чашке чая и приняв во внимание, что в каждом моле содержится число Авогадро молекул. Поскольку плотность воды р=1г/ 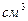, масса воды в чашке равна

.

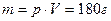Число молей в чашке равно v=m/ 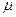=10моль. Полное число молекул в чашке чая будет

.

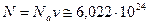В заключение этого подраздела оценим примерный размер молекулы воды. Поскольку, как только что было вычислено в задаче, в 180 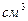содержится 10 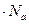молекул, на одну молекулу приходится объем

.

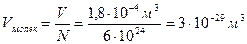Так как вода обладает очень слабой сжимаемостью, можно предположить, что молекулы практически касаются друг друга и найденный объем близок к объему самой молекулы. Поэтому можно найти линейные размеры молекулы :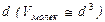

.

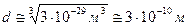Размеры молекул других веществ имеют такой же порядок величины. Вычисленный размер молекулы будет использован нами далее, при обсуждении свойств газов.

Основные понятия термодинамики

Здесь мы поясним, что понимается под различными терминами, используемыми в термодинамике. К основным понятиям термодинамики относятся: система, состояние системы, процесс, температура, внутренняя энергия, работа, количество теплоты и т.п. Часто смысл этих понятий интуитивно ясен, тем не менее ниже мы поясним, что понимается в термодинамике под каждым из этих терминов. Предлагаем вам, прочитав название очередного термина, попытаться самостоятельно сформулировать, что вы понимаете под ним, а потом прочитать его толкование и обратить внимание на то, в чем ваше понимание не совсем точно. В процессе изучения термодинамики рекомендуем вновь просмотреть толкование термина, смысл которого вам покажется не совсем ясным.

СИСТЕМОЙ (или термодинамической системой) называют любое макроскопическое тело или совокупность тел, свойства которых изучаются. Простейшим примером системы является газ, в качестве более сложного примера системы приведем жидкость и находящийся с ней в равновесии пар. Тела, не входящие в рассматриваемую систему, называются внешними телами,

или окружающей средой.

· Система называется изолированной, если она не взаимодействует с внешними телами. Строго говоря, изолированных систем не существует. Это очередная научная абстракция (как, например, понятие материальной точки), однако это допущение в каком-то конкретном случае может удовлетворительно описывать ситуацию.

· Система является не изолированной, если она взаимодействует с внешними телами. Подчеркнем, что одна и та же система может являться изолированной или не изолированной в зависимости от конкретных условий. Например, газ под поршнем может считаться изолированной системой, если поршень закреплен, а при подвижном поршне система будет, вообще говоря, не изолированной, поскольку возможно взаимодействие с атмосферным газом через силу давления, оказываемую на поршень.

СОСТОЯНИЕ системы определяется совокупностью измеряемых физических величин, называемых параметрами состояния. Параметрами состояния являются температура T, объем V, давление P.

· Равновесное состояние - это такое состояние, которое в изолированной системе сохраняется бесконечно долго. Равновесные состояния можно характеризовать определенными значениями термодинамических параметров, которые при этом постоянны по всему объему системы. При этом между термодинамическими параметрами системы имеется определенная функциональная зависимость, выражаемая уравнением состояния P=f(V,T). Конкретный вид функции f определяется из опыта. Далее мы будем иметь дело с уравнением состояния идеального газа. Равновесное термодинамическое состояние системы наглядно можно изобразить точкой в плоскости термодинамических параметров (рис. 1.1). Точка на плоскости определяется двумя координатами - термодинамическими параметрами, а третий параметр в данном случае также фиксирован и может быть найден из уравнения состояния. Термодинамика изучает в основном равновесные состояния, и поэтому ее правильней было бы назвать термостатикой.

· Состояние системы будет не равновесным }, если параметры системы меняются с течением времени. При этом термодинамические параметры разных частей системы могут быть различными, то есть система не может полностью быть охарактеризована определенным значением термодинамического параметра. Например, если температура в разных точках тела различна, то такое состояние неравновесно. Если такое тело изолировать от других тел, то температура выравняется и примет одинаковое значение T во всех точках - тело перейдет в равновесное состояние.

Первый исходный постулат термодинамики, вытекающий из опыта, состоит в том, что изолированная система с течением времени всегда приходит в состояние равновесия и никогда самопроизвольно выйти из него не может.

Процесс перехода системы из неравновесного состояния в равновесное называется процессом релаксации, или просто релаксацией, а время перехода к равновесному состоянию называют временем релаксации. Процессы релаксации выходят за рамки обычной термодинамики – их изучением занимается неравновесная термодинамика, или кинетика. В качестве примеров кинетических явлений можно назвать – такие, как теплопроводность, диффузию, внутреннее трение в жидкостях и газах.

РАВНОВЕСНЫЙ ПРОЦЕСС. Равновесное состояние неизолированной системы может изменяться в результате взаимодействия с внешними телами. Переход системы из одного состояния в другое называется процессом. Процесс будет равновесным, если при его течении система проходит через последовательные равновесные состояния. Обычно равновесные процессы вызываются медленными изменениями внешних условий, так что очередное равновесное состояние успевает установиться (то есть когда характерное время изменения внешних условий должно быть много больше, чем соответствующее время релаксации). Ясно, что равновесный процесс в плоскости термодинамических параметров изобразится линией, каждая точка которой соответствует равновесному состоянию. Эта линия представляет собой график равновесного процесса. На рис. 1.1. изображен график процесса перехода из состояния 1 в состояние 2.

Р

1 2

V

Рис. 1.1. График равновесного процесса

· Равновесный процесс является обратимым процессом, поскольку он может быть проведен в обратном направлении, когда система проходит через те же равновесные состояния в обратной последовательности. На графике процесса (рис. 1.1) этому соответствует движение в обратном направлении от точки 2 к точке 1.

· Процесс, при котором система после ряда изменений возвращается в исходное состояние, называется круговым процессом, или циклом. График кругового процесса представляет собой замкнутую кривую (рис. 1.2).

ТЕМПЕРАТУРА является одним из основных термодинамических параметров, определяющих состояние системы. Существование такого параметра, определяющего направление самопроизвольной передачи тепла, является вторым постулатом термодинамики.

Р

1 2

V

Рис. 1.2. График равновесного цикла

Поскольку температура определяет состояние системы вместе с другими термодинамическими параметрами, для ее определения можно следить за какими-либо термодинамическими параметрами, которые можно легко измерять. В большинстве термометров (например, в жидкостных) используется свойство тел увеличивать свой объем с ростом температуры. Если за ноль температуры принять температуру таяния льда, а температуру кипения воды при атмосферном давлении - за 100 градусов, получим температурную шкалу Цельсия, наиболее применимую в быту. Более точно можно измерять температуру, если в качестве термометрического тела использовать газ и следить за его давлением в заданном объеме. Тогда давление будет линейно увеличиваться с ростом температуры t:

,

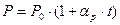где буквой t обозначена температура по шкале Цельсия, 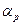- так называемый термический коэффициент давления. Удивительно, что для любых достаточно разреженных газов 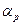имеет одно и то же значение: 1/273,16. Это позволяет ввести более удобную в теории шкалу температур T - шкалу Кельвина:

.

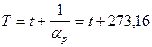Видим, что величина градусов в этих шкалах совпадает (увеличение t на один градус приводит к увеличению T также на один градус). Однако начало отсчета (ноль температуры) не совпадают - 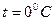(ноль по шкале Цельсия) соответствует T = 273,16 K. Удобство шкалы Кельвина видно уже из того, что зависимость давления газа от температуры при постоянном объеме (закон Шарля) становится проще: .

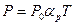Предложение к размышлению. Для более глубокого усвоения этого вопроса предлагаем вам самостоятельно ответить на вопрос: можно ли было бы ввести температурную шкалу Кельвина, если бы 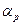имел разное значение для разных газов? Если вы затруднитесь с ответом или захотите проверить свой

ответ, прочитайте сноску на стр. 12.

ВНУТРЕННЯЯ ЭНЕРГИЯ системы является суммой всех видов энергии, заключенных в этой системе. Согласно первому постулату термодинамики внутренняя энергия изолированной системы остается постоянной, какие бы процессы в ней ни происходили. Это, в частности, означает, что каждое состояние системы характеризуется определенным значением внутренней энергии. Всякий раз, когда система оказывается в этом состоянии, внутренняя энергия принимает фиксированное значение. Другими словами, внутренняя энергия является функцией состояния.

Внутренняя энергия обладает свойством аддитивности (от английского глагола add - добавлять, складывать), т.е. внутренняя энергия системы равна сумме внутренних энергий ее частей.

Полная энергия E любого тела может быть представлена в виде суммы внутренней энергии U и механической энергии движения тела как целого 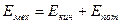. Иначе говоря, при вычислении внутренней энергии не учитывают движение тела (системы) как целого.

Значение других важных термодинамических терминов мы поясним по мере их появления.

Date: 2015-05-09; view: 1266; Нарушение авторских прав