Работа, производимая термодинамической системой

Понятие физической работы вводилось при изучении раздела <<механика>> (предлагаем вам вновь просмотреть соответствующий материал). В термодинамике состояние системы и работу, совершаемую системой принято выражать через термодинамические параметры. В данном разделе будет получено соответствующее выражение.

Рассмотрим газ, заключенный в цилиндр с легко скользящим (без трения) поршнем (см. рис. 1.2). Пусть газ расширился, при этом поршень переместился вверх на величину dx. Элементарная работа газа при расширении равна:

dA=F × dx,

где F - сила давления на поршень. Выразим F через давление газа р и площадь поршня s:

F=p × s.

S

DV Dx

p, V

Рис. 2.1. Схема вычисления работы при расширении газа

Тогда dA = р × s dx, а учитывая, что s d=dV - приращение объема газа, получим:

dA=p × dV. (2.1)

Если dV >0, то и dA >0 и говорят, что работу совершает газ; если dV <0, то dA <0 и в этом случае работа совершается над газом, поскольку в последнем случае будет положительной работа внешних сил (по III закону Ньютона внешние силы равны силам давления газа, но имеют противоположное направление, поэтому их работа отличается знаком от работы газа). В частности, при изохорическом процессе, когда V=const, dV =0, элементарная работа dA =0. Это обстоятельство аналогично механической ситуации, когда при наличии силы тело покоится и, следовательно, не совершает работу.

Изобразим процесс изменения объема газа графически в координатах {р,V}. Пусть начальное состояние газа соответствует точке 1 со значениями р₁, V₁, а конечное состояние - точке 2 со значениями р₂, V₂. Процесс графически можно представить кривой, соединяющей точки 1 и 2 (кривая а на рис. 2.2). Элементарная работа dA, определяемая формулой (2.1), равна площади заштрихованной площадки. Полная работа A_1-2 равна сумме всех элементарных работ от точки 1 до точки 2 и может быть найдена путем вычисления интеграла:

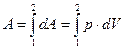(2.2)

и эквивалентна всей заштрихованной области, лежащей под кривой, изображающей процесс (в нашем случае 1-а-2). В случае обратного процесса 2-а-1 работа изображается той же площадью, но имеет противоположный знак (в этом случае dv отрицательно).

Если бы газ переходил из состояния 1 в состояние 2 по кривой 1-b-2 (см. рис. 2.3), лежащей ниже кривой 1-a-2, то работа газа была бы меньше. Следовательно, работа, совершаемая газом в процессе перехода из одного состояния в другое, зависит от того, как именно, по какому пути, через какие промежуточные состояния совершился этот переход.

p

p₁

p

p₂

V

V₁ DV u₂

Рис. 2.2. Работа системы при ходе процесса

Если газ совершил цикл 1-a-2-b-1, то несмотря на то, что система возвращается в исходное состояние, работа при этом круговом процессе не равна нулю:

.

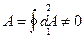Таким образом, работа, в отличие от внутренней энергии, не является функцией состояния системы и dA не может рассматриваться как полный дифференциал некоторой функции A. Для того, чтобы подчеркнуть это обстоятельство, в термодинамике элементарную работу изображают dA (в отличие от дифференциала внутренней энергии dU).

p a

1 2

b

V

C D

Рис. 2.3. Работа кругового процесса

Date: 2015-05-09; view: 683; Нарушение авторских прав