Средняя энергия теплового движения молекул равна кинетической энергии

молекулы, движущейся со средней квадратичной скоростью.

В действительности молекулы могут иметь не дискретные, а непрерывные значения скоростей. Следовательно, в реальности число групп k молекул, имеющих разные скорости, бесконечно велико k ®¥. В этом случае относительные доли числа молекул N₁/N, N₂/N, …, имеющих соответствующие скорости, следует заменить аналогичной величиной dF(u):

,

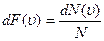которая равна числу молекул, имеющих величину модуля скорости большую u -d u, и меньшую u + du, деленную на полное число частиц. Понятно, что чем больше величина du, тем больше dF (u): dF (u)= f (u) du, где f (u) - функция, характеризующая распределение молекул по величине скорости.

С учетом сказанного формула (1.14) в этом случае может быть переписана в виде (сумма преобразуется в интеграл):

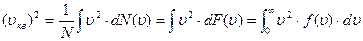, (1.15)

причем интегрирование проводится по всем возможным значениям модуля скорости.

В случае идеального газа, находящегося в тепловом равновесии, функция f (u) была получена Дж.. Максвеллом и имеет вид:

,

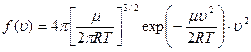где m - молярная масса газа, а T - равновесная температура. Таким образом, величина (u_кв)² для одноатомного идеального газа определится значением интеграла[2]

.

Таким образом, средняя квадратичная скорость молекул одноатомного газа равна:

.

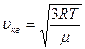Далее мы получим этот результат элементарными методами, что показывает справедливость упрощенного подхода, примененного при выводе основного уравнения молекулярно-кинетической теории.

Сопоставление с уравнением Клайперона - Менделеева. Воспользовавшись тем, что концентрация молекул n=N/V, основное уравнение молекулярно-кинетической теории можно записать в виде:

.

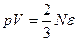Сравнивая это выражение с уравнением состояния идеального газа (1.11),

приходим к выводу, что:

.

С другой стороны, число молекул газа можно выразить через число молей и число Авогадро: N=nN_а= 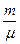N_а. Поэтому для средней кинетической энергии молекул получим формулу:

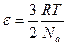. (1.16)

Напомним, что согласно формуле (1.8), универсальная газовая постоянная R относится к одному молю газа, содержащему N _а молекул. Из последнего выражения видно, что удобно ввести новую постоянную k, представляющую собой универсальную газовую постоянную в расчете на одну молекулу:

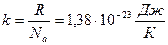(1.17)

Фундаментальная постоянная k называется постоянной Больцмана.

Теперь формулу (1.16) можно записать в виде:

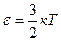. (1.18)

Интересно, что средняя кинетическая энергия молекул газа определяется только температурой газа. Следовательно, если два газа имеют молекулы разной массы, то среднеквадратичная скорость больше у газа с более легкими молекулами.

В заключение данного пункта приведем альтернативную форму уравнения состояния идеального газа, которую можно получить, если в уравнении (1.11) заменить универсальную газовую постоянную, воспользовавшись выражением (1.17):

р=nkT. (1.19)

Такое же соотношение получится, если подставить величину e из формулы (1.18) в основное уравнение молекулярно-кинетической теории.

Date: 2015-05-09; view: 784; Нарушение авторских прав