Регулярный режим теплопроводности

Охлаждение однородного изотропного тела произвольной формы в среде с постоянной температурой и постоянным коэффициентом теплоотдачи на его поверхности во времени определяется дифференциальным уравнение теплопроводности

и граничными условиями

.

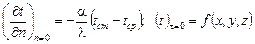Решение дифференциального уравнения при 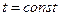показывает, что температура в любой точке изменяется по экспоненциальному закону

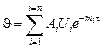, (20.4)

где 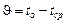; 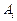- постоянные, зависящие от формы тела и начального распределения температур; - функции координат, характеризующие изменение температуры в пространстве; 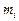- постоянные, представляющие собой ряд положительных возрастающих чисел ().

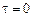Анализ уравнения (20.4) показывает, что при малых значениях от ( до 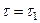) процесс охлаждения (нагревания) зависит от начальных условий охлаждения и имеет случайный характер, не связанный с условиями охлаждения. Этот период охлаждения определяется не только первым, но и последующими членами ряда (20.4). Эту стадию охлаждения называют первым периодом охлаждения (или неупорядоченным процессом).

С увеличением времени ряд быстро сходится и все члены его, кроме первого, стремятся к нулю. При , превышающем некоторое определенное значение 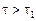, начальные условия начинают играть второстепенную роль, и процесс полностью определяется только начальными условиями на поверхности тела, его физическими свойствами, геометрической формой и размерами. Вторая стадия охлаждения называется регулярным режимом и описывается первым членом ряда (20.4), т.е.

.

Логарифмируя это уравнение, имеем

.

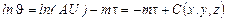Из последнего уравнения видно, что регулярный режим нестационарной теплопроводности характеризуется тем, что натуральный логарифм избыточной температуры 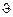любой точки тела изменяется во времени по линейному закону.

После дифференцирования обеих частей уравнения по времени, получаем: 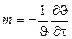, с^-1.

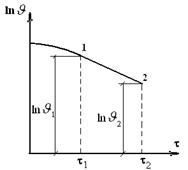
Относительная скорость изменения температуры в единицу времени в любой точке тела не зависит от координат и времени. Величину 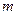называют темпом регулярного режима и определяют из опыта. Если взять внутри тела произвольную точку и измерять температуру в этой точке, то процесс охлаждения будет выражаться кривой, рис. 20.2

Рис. 20.2. Кривая изменения натурального логарифма избыточной

температуры при регулярном режиме теплопроводности

Величина темпа 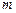определяется тангенсом угла наклона прямой части графика к оси абсцисс:

.

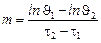Теория регулярного режима теплопроводности применима к телам любой формы. Она позволяет установить связь процесса регулярного режима с его физическими и геометрическими параметрами и внешними условиями теплообмена. В общем случае 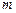определяется из уравнения

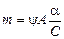, с^-1,

т.е. темп 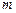, характеризующий скорость изменения температуры тела, прямо пропорционален коэффициенту теплоотдач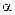и (если 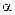не стремится к бесконечности) поверхности тела 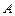и обратно пропорционален его полной теплоемкости 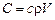; 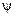- безразмерный коэффициент пропорциональности, характеризующий неравномерность распределения температуры в теле и являющийся функцией числа Био.

Это уравнение выражает закон сохранения энергии для охлаждающегося тела в среде с постоянной температурой. Если 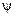= 1, то распределение температуры в теле - равномерно; если 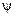= 0, то распределение температур становится неравномерным (температура поверхности равна температуре среды, а температура внутри тела не равна температуре его поверхности).

Если коэффициент теплоотдачи , то 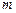прямо пропорционален температуропроводности тела:

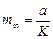, или ,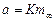

где 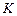- коэффициент пропорциональности, зависящий от геометрических размеров и формы тела, м².

Например, для шара 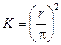; для цилиндра 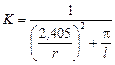(где 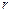- радиус, 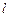- длина цилиндра).

На основе теории регулярного режима теплопроводности разработаны методы определения теплофизических величин для твердых и жидких тел (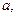 λ, с).

Date: 2015-05-09; view: 1342; Нарушение авторских прав