Неограниченная пластина

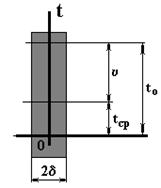
Рис.20.1. Схема пластины бесконечной длины

В начальный момент времени пластина имеет во всех точках постоянную температуру t_o, поэтому и избыточная температура J₁ = t_o – t_cp будет постоянной во всех точках пластины. Кроме того, заданы коэффициент теплопроводности l_ст, плотность тела и его теплоемкость 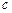. Коэффициент температуропроводности: 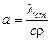, Вт/м²×К. Так как пластина безгранична по длине и по ширине, то дифференциальное уравнение теплопроводности Фурье принимает вид

.

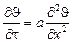Граничное условие х = ± d. 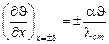, и начальное условие J = J₁.

Температура поверхности пластины и в ее средней плоскости определяется из соотношения

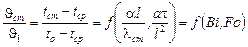. (20.1)

Безразмерная координата 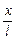в средней плоскости и на поверхности пластины есть величина постоянная и поэтому отсутствует в уравнении (14.1), при х = 0 ® 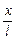= 0; при х = d ® 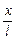= 1.

Температура пластины в средней плоскости

. (20.2)

Количество теплоты, которое отдает (или воспринимает) пластина в окружающую среду за время t равно изменению внутренней энергии.

Начальная внутренняя энергия пластины равна

.

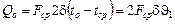За время t внутренняя энергия составит

,

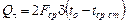где Q_t - количество теплоты, переданное в окружающую среду за время t, Дж; t_cp.ст – средняя температура пластины по истечении времени t, °С.

. (20.3)

Зависимости (20.1), (20.2) и (20.3) даются в виде графиков или в виде таблиц. Значения 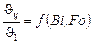, , 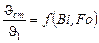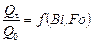для неограниченной пластины приведены в табл. 20.1 – табл. 20.3.

Date: 2015-05-09; view: 718; Нарушение авторских прав