
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Цилиндр бесконечной длины
|
|
Задача на охлаждение цилиндра аналогична задаче на охлаждение бесконечной пластины, поэтому:
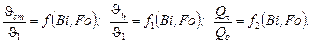
Внутренняя энергия рассматриваемого участка цилиндра длиной l, отсчитанная от ее значения при температуре среды, как от нуля, определяется по формуле
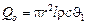 .
.
Для цилиндрической стенки 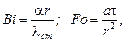 где r – радиус цилиндра.
где r – радиус цилиндра.
Величины 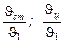 и
и 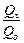 как функции числа Bi и числа Fo для цилиндра бесконечной длины приведены в табл. 20.4 – табл.20.6.
как функции числа Bi и числа Fo для цилиндра бесконечной длины приведены в табл. 20.4 – табл.20.6.
Таблица 20.1
Значения отношений избыточных температур 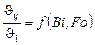
в средней плоскости неограниченной пластины
| Fo\Bi | .0001 | .001 | .01 | .1 | .5 | |||||
| .02 .05 .1 .5 | - - - - - - - | - - - .99 .98 .96 | - - .99 .99 .98 .95 .9 .82 .61 | - - .97 .92 .83 .62 .37 .14 .01 | - - .1 .87 .7 .46 .13 .02 - | - - .78 .54 .31 .03 - - | - .98 .56 .25 .06 - - - | - .97 .46 .16 .02 - - - | - .1 .96 .41 .13 .01 - - - | - .1 .95 .39 .12 .01 - - - |
Таблица 20.2
Значения отношений избыточных температур 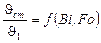
на поверхности неограниченной пластины
| Fo\Bi | .0001 | .001 | .01 | .1 | .5 | |||||
| .02 .05 .1 .5 | - - - - - - - | - .99 .98 .95 | .99 .99 .99 .99 .98 .95 .9 .82 .61 | .99 .97 .96 .93 .88 .8 .6 .37 .14 .01 | .95 .87 .82 .71 .67 .36 .1 .01 - | .89 .77 .69 .53 .35 .16 .02 - - | .66 .42 .31 .17 .07 .01 - - - | .42 .21 .14 .06 .02 - - - - | .24 .1 .06 .03 .01 - - - - - | .11 .05 .03 .01 - - - - - |
Таблица 20.3
Значения относительного изменения внутренней энергии 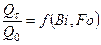 для неограниченной пластины
для неограниченной пластины
| Fo\Bi | .0001 | .001 | .01 | .1 | .2 | .5 | ||||
| .02 .05 .1 .5 | - - - - - - - - - .01 | - - - - - - - .01 .02 .04 | - - - - .01 .02 .05 .1 .18 .39 | - .01 .02 .05 .1 .17 .39 .62 .81 .92 | - .01 .03 .09 .17 .31 .63 .84 .93 .99 | .01 .02 .05 .2 .35 .59 .88 .99 - | .02 .04 .08 .32 .53 .78 .98 - - | .05 .12 .2 .58 .81 .96 - - - | .09 .18 .27 .69 .89 .98 - - - | .12 .23 .34 .75 .92 .99 - - - |
Шар
Дифференциальное уравнение теплопроводности для шара имеет вид
 .
.
Задача охлаждения аналогична предыдущим – охлаждению бесконечной пластины и цилиндра. Относительные разности температур определяются как функции чисел Bi и Fo, т.е.
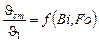 ;
; 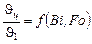 ;
; 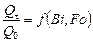 .
.
Значения числа Био и числа Фурье для шара рассчитываются по формулам:
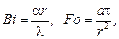
где r – радиус шара.
Зависимости между безразмерными величинами определяются по табл. 20.7 - табл.20.9, а затем по найденным величинам относительных разностей температур и относительного теплового потока находятся температуры стенки шара - tст, температуры в центре шара – tц и отданная теплота - Qt. Начальная внутренняя энергия шара рассчитывается по формуле
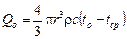 .
.
Таблица 20.4
Значения отношений избыточных температур
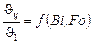 для цилиндра бесконечной длины
для цилиндра бесконечной длины
| Fo\Bi | .0001 | .001 | .01 | .1 | .5 | |||||
| .01 .05 .1 .25 .5 2.5 | - - - - - - - | - - - - - - .99 .98 .95 | - - - .99 .98 .95 .91 .82 .61 | - - .98 .93 .84 .63 .38 .14 .01 | - .99 .89 .72 .46 .12 .01 | - .97 .81 .55 .25 .02 - - | - .94 .59 .24 .04 - - - | .99 .9 .48 .15 .01 - - - | .99 .88 .43 .12 .01 - - - | .99 .87 .4 .1 .01 - - - |
Таблица 20.5
Значения отношений избыточных температур
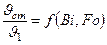 на поверхности цилиндра бесконечной длины
на поверхности цилиндра бесконечной длины
| Fo\Bi | .0001 | .001 | .01 | .1 | .5 | |||||
| .01 .05 .1 .25 .5 2.5 | - - - - - - - | - .99 .98 .95 | .99 .99 .99 .99 .98 .95 .9 .82 .61 | .99 .97 .96 .93 .88 .8 .6 .37 .14 .01 | .95 .87 .82 .71 .67 .36 .1 .01 - | .89 .77 .69 .53 .35 .16 .02 - - | .66 .42 .31 .17 .07 .01 - - - | .42 .21 .14 .06 .02 - - - - | .24 .1 .06 .03 .01 - - - - - | .11 .05 .03 .01 - - - - - |
Таблица 20.6
Значения относительного изменения внутренней энергии 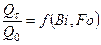 для цилиндра бесконечной длины
для цилиндра бесконечной длины
| Fo\Bi | .0001 | .001 | .01 | .1 | .5 | |||||
| .01 .05 .1 .25 .5 2.5 | - - - - - - - - - - | - - - - - - - .01 .02 .04 | - - - - .01 .02 .05 .09 .18 .39 | - .01 .02 .05 .09 .18 .39 .62 .86 .99 | .01 .05 .09 .2 .36 .59 .89 .99 | .02 .08 .15 .33 .55 .79 .98 | .05 .21 .37 .62 .85 .98 | .11 .32 .48 .75 .92 .99 | .15 .38 .54 .79 .94 | .18 .42 .58 .81 .95 |
Таблица 20.7
Значения отношений избыточных температур
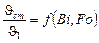 для шара
для шара
| Fo\Bi | .0001 | .001 | .01 | .1 | .5 | |||||
| .01 .05 .1 .25 .5 2.5 | .99 .99 .97 .94 | .99 .99 .99 .98 .97 .93 .86 .75 .48 | .99 .97 .95 .92 .85 .73 .52 .23 .05 | .94 .86 .79 .64 .46 .23 .03 - - | .89 .75 .64 .44 .24 .07 - - - | .64 .39 .26 .1 .02 - - - - | .38 .17 .1 .03 - - - - - | .22 .09 .05 .01 - - - - - | .1 .03 .02 - - - - - - |
Таблица 20.8
Значения отношений избыточных температур 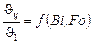 для шара
для шара
| Fo\Bi | .0001 | .001 | .01 | .1 | .5 | |||||
| .01 .05 .1 .25 .5 2.5 | - - - - - - | - - - .99 .99 .98 .94 | - - .99 .99 .97 .93 .87 .75 .49 | - .99 .97 .89 .77 .55 .24 .06 | - .97 .81 .58 .29 .04 - - | - .95 .69 .37 .11 - - - | .98 .87 .38 .09 - - - - | .98 .8 .26 .03 - - - - | .98 .76 .22 .02 - - - - | .97 .73 .19 .02 - - - - |
Таблица 20. 9
Значения относительного изменения внутренней энергии 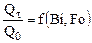 для шара
для шара
| Fo\Bi | .0001 | .001 | .01 | .1 | .5 | |||||
| .01 .05 .1 .25 .5 2.5 | - - - - - - - - - - | - - - - - - - .01 .02 .05 | - - - .01 .02 .03 .08 .15 .27 .56 | .02 .03 .07 .14 .25 .52 .77 .95 .99 | .02 .07 .13 .29 .49 .74 .97 - - | .03 .12 .23 .47 .71 .92 - - - | .09 .32 .51 .8 .96 - - - - | .16 .46 .66 .9 .99 - - - - | .22 .53 .71 .92 .99 - - - - | .27 .57 .75 .91 .99 - - - - |
Пример 20.1
Определить температуру на поверхности и в центре равномерно нагретого до 927 °С весьма длинного стального цилиндра диаметром 400 мм через 1 час и через 0,5 часа после помещения его на воздухе с температурой 27 °С. Коэффициент теплоотдачи от стенки цилиндра к воздуху a = 5 Вт/м2×К, коэффициент теплопроводности стали l = 50 Вт/м×К, теплоемкость стали с = 0,71 кДж/кг×К, плотность стали r = 7900 кг/м3.
Решение.
1. Определим температуру спустя 1 час после помещения цилиндра на воздухе:
- коэффициент температуропроводности
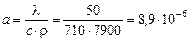 , м2/с;
, м2/с;
- число Био:
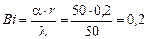 ;
;
- число Фурье: 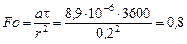 .
.
По значениям числа Bi и Fo из табл. 20.4 и табл. 20.5 находим для цилиндра:
 .
.
Разность температур:
J1 = to – tcp = 927 – 27 = 900 °C.
Температуры поверхности и на оси цилиндра через 1 час:
Jcт = 0,74×900 = 666 °С, tст = Jст + tст = 666 + 27 = 693 °С;
Jц = 0,8×900=720 °С, tц = Jц + tcp = 720 + 27 = 747 °C.
2. Потери теплоты за 1 час: 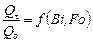 .
.
По табл. 20.6 для цилиндра находим 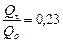 , или потеря теплоты через 1 час составляет 23 % от начальной внутренней энергии цилиндра.
, или потеря теплоты через 1 час составляет 23 % от начальной внутренней энергии цилиндра.
3. Определим tcт, tц и 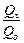 через 0,5 часа после помещения цилиндра на воздухе.
через 0,5 часа после помещения цилиндра на воздухе.
Числа Био и Фурье: Bi = 0,2; Fo = 0,4.
По таблицам находим 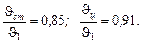
Разность температур - J1 = to – tcp = 927 – 27 = 900 °C.
Температура поверхности - Jcт = 0,85×900 = 765 °С, tст = Jст + tст = 765 + 27 = 693 °С.
Температура на оси цилиндра - Jц = 0,91×900 = 819 °С, tц = Jц + tcp = 819 + 27 = 846 °C.
Потери теплоты из табл. 20.9 - 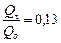 .
.
Date: 2015-05-09; view: 1454; Нарушение авторских прав