Основные законы теплового излучения

Закон Планка.

Планк теоретически, исходя из электромагнитной природы излучения и используя представления о квантах энергии, установил закон изменения интенсивности излучения абсолютно черного тела в зависимости от температуры и длины волны

,

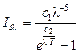где 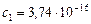Вт/м² – первая постоянная Планка; 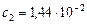м∙К – вторая постоянная Планка; 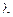- длина волны; 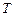- температура излучающего тела, К.

Из рис. 18.1 видно, что для любой температуры интенсивность излучения 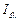возрастает от 0 при 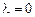до своего максимального значения 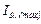при определенной длине волны 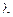, а затем убывает до 0 при 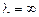. При повышении температуры интенсивность излучения для каждой длины волны возрастает. Кроме того, с повышением температуры максимумы кривых смещаются в сторону коротких волн.

Длина волны 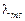(мм) соответствующая максимальной интенсивности излучения определяется законом Вина

,

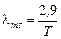т.е., с увеличением температуры длина волны 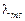, соответствующая максимальной интенсивности 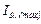уменьшается.

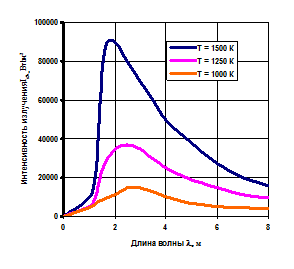
Рис. 18.1. Графическая зависимость изменения интенсивности излучения

абсолютно черного тела от длины волны и температуры

(к закону Планка)

Закон Стефана-Больцмана.

На основании опытных данных Стефан в 1879 г. установил, что поверхностная плотность энергии излучения абсолютно черного тела прямо пропорциональна четвертой степени абсолютной температуры

.

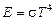В 1884 г. Больцман получил этот закон теоретическим путем, исходя из второго закона термодинамики и допущения существова-

ния светового давления.

Для вывода аналитического выражения указанного закона воспользуемся термодинамическим тождеством

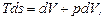
из которого следует, что

, (*)

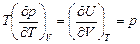где 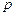- световое давление, 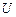- энергия равновесного излучения объема .

Согласно законам электродинамики, рассматривающим равновесное излучение как фотонный газ, световое давление можно выразить как

, (**)

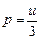где 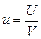- объемная плотность, равновесного излучения.

Тогда после преобразований, учитывая, что , уравнение (*) приводится к виду

.

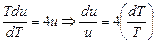После интегрирования и последующего потенцирования получим

. (***)

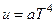Связь между объемной плотностью равновесного излучения 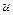и поверхностной плотностью излучения 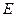устанавливается соотношением

, (****)

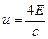где 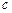- скорость движения фотонов, равная скорости света в пустоте. Подставляя в (***) значение 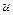из (****), получим

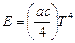или ,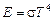

где 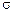- коэффициент пропорциональности (постоянная Стефана-

Больцмана).

Аналитическое выражение закона Стефана-Больцмана также можно получить, используя закон Планка, в соответствии с которым поверхностная плотность энергии излучения абсолютно черного тела записывается уравнением

.

Интегрируя это уравнение в пределах от 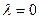до 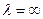, получим

.

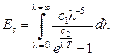Раскладывая подынтегральное выражение в ряд, и интегрируя его, найдем расчетную формулу для поверхностной плотности энергии излучения абсолютно черного тела

,

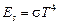где 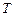- термодинамическая температура, 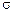- постоянная Стефана-Больцмана.

Так как 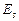выражается в , 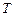- в К, то 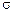выразится в 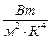. Постоянная 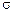определяется опытным путем

.

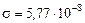
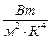Уравнение в рамке является аналитическим выражением закона Стефана-Больцмана, т.е. поверхностная плотность энергии излучения (излучательность) черного тела пропорциональна абсолютной температуре в четвертой степени.

Обычно в технической литературе закон Стефана-Больцмана записывается в виде

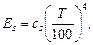
где 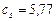- коэффициент излучения абсолютно черного тела, .

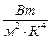Все реальные тела, используемые в технике, не являются абсолютно черными и при одной и той же температуре излучают меньше энергии, чем абсолютно черное тело. Излучение реальных тел также зависит от температуры и длины волны.

Чтобы законы излучения черного тела можно было применить для реальных тел, вводится понятие о сером теле и сером излучении. Под серым излучением понимают такое, которое, аналогично излучению черного тела, имеет сплошной спектр, но спектральная излучательность для каждой длины волны 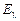при любой температуре составляет неизменную долю спектральной излучательности черного тела 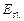. Следовательно, должно существовать следующее соотношение:

.

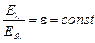Величину 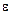называют коэффициентом черноты. Он зависит только от физических свойств тела. Степень черноты серых тел всегда меньше единицы.

Большинство реальных твердых тел с определенной степенью точности можно считать серыми телами, а их излучение – серым излучением.

Излучательность серого тела

,

но 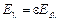, поэтому

,

где 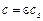- коэффициент излучения серого тела. Величина 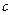реальных тел в общем случае зависит не только от физических свойств тела, но и от состояния поверхности или от ее шероховатости, а также от температуры и длины волны. Значения коэффициентов черноты 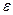для различных материалов приводятся в специальных таблицах.

Закон Кирхгофа.

Для всякого тела энергия излучения и энергия поглощения зависят от температуры и длины волны. Различные тела имеют различные 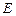и 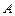. Зависимость между ними устанавливается законом Кирхгофа.

Рассмотрим теплообмен излучением между двумя параллельными пластинами с различными температурами, причем одна из пластин абсолютно черная с температурой 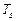, а вторая серая с температурой 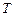. Расстояние между пластинами значительно меньше их размеров, так что излучение каждой из них обязательно попадает на другую.

Вторая пластина излучает на первую по закону Стефана-Больцмана энергию 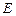, которая полностью поглощается черной пластиной. С другой стороны первая пластина излучает на вторую энергию 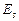, часть которой поглощается, а остальная энергия 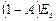отражается на первую и ею полностью поглощается. При этих условиях серая поверхность получает энергию в количестве 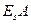, а расходует 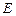. Следовательно, уравнение теплового баланса будет иметь вид

.

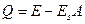Предположим, что температуры пластин раны между собой, тогда тепловой поток будет равен нулю - . Отсюда получаем

.

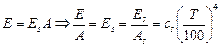Так как вместо серого тела можно взять любое другое, то полученное уравнение справедливо для любых тел и является математическим выражением закона Кирхгофа.

Отношение излучательной способности тела к его поглощательной способности одинаково для всех серых тел, находящихся при одинаковых температурах, и равно излучательной способности абсолютно черного тела при той же температуре.

Из закона Кирхгофа следует, что если тело обладает малым коэффициентом поглощения, то оно одновременно обладает и малой излучательностью (малой поверхностной плотностью энергии излучения), например полированные металлы. Абсолютно черное тело, обладающее максимальным коэффициентом поглощения, имеет и наибольшую излучательность (поверхностную плотность энергии излучения).

Закон Кирхгофа остается справедливым и для монохроматического излучения. Отношение спектральной излучательности тела при определенной длине волны 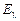к его коэффициенту поглощения при той же длине волны 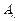для всех тел одно и то же, если они находятся при одинаковых температурах 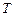, и численно равно спектральной излучательности абсолютно черного тела 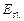при той же длине волны 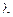и температуре 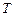, т.е. является функцией только длины волны и температуры:

.

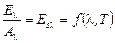Отсюда следует, что тело, которое излучает поток энергии при какой-нибудь длине волны, способно поглощать его при этой же длине волны. Если тело не поглощает энергию в какой-нибудь части спектра, то оно в этой части спектра и не излучает.

Из закона Кирхгофа также следует, что коэффициент черноты серого тела 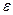численно равен коэффициенту поглощения :

.

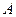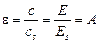Закон Ламберта.

Энергия, излучаемая телом, распространяется в пространстве с различной интенсивностью, которая зависит от направления.

Согласно закону Ламберта количество энергии, излучаемое некоторым элементом поверхности 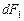в направлении элемента 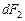, пропорционально произведению количества энергии, излучаемого по нормали 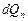, на величину пространственного угла 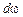и 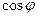, составленного направлением излучения и нормалью 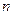, рис. 18.2:

,

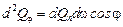или

, (*)

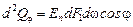где 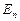- энергия излучения в направлении нормали.

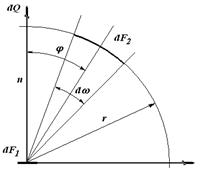
Рис. 18.2. Схема распространения потока лучистой энергии

в пространстве (к закону Ламберта)

Следовательно, наибольшее количество энергии излучается в перпендикулярном направлении к поверхности излучения, т.е. пр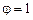и и 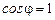. С увеличением угла 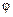количество энергии излучения уменьшается и при 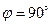становится равным нулю, т.к. 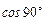= 0.

Для определения величины 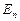необходимо полученное уравнение проинтегрировать по поверхности полусферы, лежащей над плоскостью 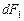. Окончательная формула для энергии излучения в направлении нормали 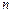будет иметь вид

,

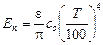где 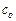- коэффициент излучения при .

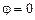Из приведенного уравнения следует, что энергия излучения в направлении нормали в 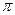раз меньше энергии излучения абсолютно черного (или серого) тела, определяемого по закону Стефана-Больцмана, поэтому уравнение закона Ламберта (*) принимает вид

.

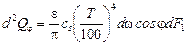Полученная формула справедлива как для потока энергии излучения элемента поверхности 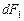, так и для монохроматического излучения и является основной для расчета теплообмена излучением между поверхностями конечных размеров.

Закон Ламберта полностью справедлив для абсолютно черного или серого тела, а для тел, обладающих диффузным излучением, - только в пределах 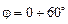. Для полированных поверхностей закон Ламберта неприменим.

Date: 2015-05-09; view: 1181; Нарушение авторских прав