
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение 3.8
|
|
Векторным произведением векторов ` а и ` b называется вектор` v, удовлетворяющий свойствам:
а) | 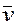 | = |
| = |  |.|
|.|  |. sin
|. sin 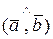 ,
,
б) вектор` v перпендикулярен плоскости, в которой лежат векторы  и
и  ;
;
в) векторы  ,
,  ,` v, взятые в указанном порядке, образуют правую тройку
,` v, взятые в указанном порядке, образуют правую тройку
Векторное произведение обозначается  ´
´  или [
или [  ,
,  ]. Векторное произведение обладает свойствами:
]. Векторное произведение обладает свойствами:
1) 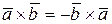 ,
,
2) 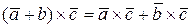 ,
,
3) 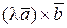 = l(
= l(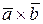 ) =
) = 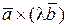 ,
,
4) 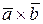 =`0 (
=`0 ( ¹`0,
¹`0,  ¹`0) тогда и только тогда, когда векторы
¹`0) тогда и только тогда, когда векторы  и
и  коллинеарны. В частности,
коллинеарны. В частности, 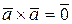 .
.
Для базисных векторов ` i,` j,` k имеют место соотношения:

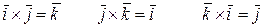
 .
.
Пусть векторы заданы своими координатами:
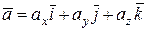 и
и 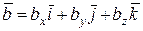 .
.
Используя перечисленные свойства, получим
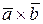 =
= 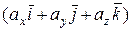 ´
´ 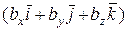 =
= 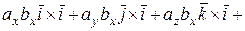
+ 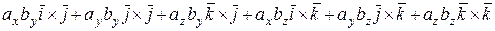 =
=
= 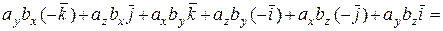
= 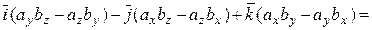
= 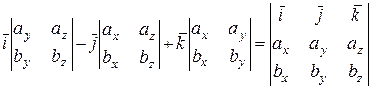 .
.
Таким образом, через координаты перемножаемых векторов ` a = (ax, ay, az) и ` b = (bx, by, bz) векторное произведение может быть записано в виде символического определителя
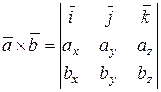 .
.
или в виде координатной строки
 ´
´  =
= 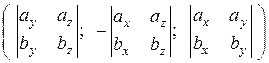 .
.
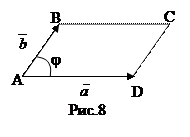 Рассмотрим параллелограмм ABCD, построенный на векторах` а и` b как на сторонах (рис. 8). Площадь этого параллелограмма равна
Рассмотрим параллелограмм ABCD, построенный на векторах` а и` b как на сторонах (рис. 8). Площадь этого параллелограмма равна
Sпар. = |AB|.|AD|.sinj = |  |.|
|.|  |. sinj = |
|. sinj = |  ´
´  |.
|.
Таким образом, с геометрической точки зрения, модуль векторного произведения двух неколлинеарных векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.
Date: 2015-04-23; view: 529; Нарушение авторских прав