
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение 3. 6
|
|
Число, равное произведению длин двух векторов на косинус угла между ними называется скалярным произведением этих векторов. Для векторов  и
и 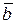 их скалярное произведение обозначается (
их скалярное произведение обозначается ( ,
,  ), или
), или  .
.  .
.
Таким образом, по определению
 .
.  = |
= |  |.|
|.|  | cos
| cos 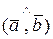 .
.
Скалярное произведение обладает свойствами:
1.  .
.  =
=  .
.  ;
;
2.  . (
. ( + `с) =
+ `с) =  .
.  +
+ 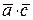 ;
;
3.  .
.  = |
= |  |2 =
|2 =  2 – скалярный квадрат; отсюда
2 – скалярный квадрат; отсюда 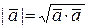 ;
;
4. l  .
.  = (l
= (l  ) .
) .  =
=  . (l
. (l  );
);
5.  .
.  = 0 тогда и только тогда, когда хотя бы один из векторов нулевой, либо когда векторы
= 0 тогда и только тогда, когда хотя бы один из векторов нулевой, либо когда векторы  и
и  ортогональны;
ортогональны;
6. 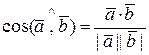 . Пользуясь этим свойством, получим
. Пользуясь этим свойством, получим
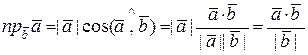 .
.
Заметим, что для ортонормированного базиса {` i,` j,` k } пространства V3 справедливы следующие соотношения
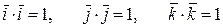 ,
,
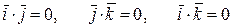 .
.
Пусть в ДПСК, порожденной репером [O,` i,` j,` k ], заданы два вектора
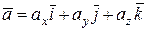 и
и 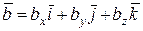 .
.
Используя перечисленные свойства скалярного произведения, получим для этих векторов:
 .
.  =
= 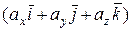 .
. 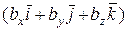 =
= 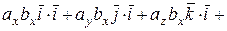
+ 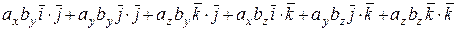 =
=
= 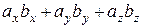 .
.
Таким образом, если векторы заданы своими координатами в ДПСК, то их скалярное произведение равно сумме произведений соответствующих координат этих векторов:
 .
.  =
= 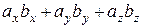 .
.
Пользуясь этим правилом, можно записать в координатной форме
|  | = (
| = ( .
.  ) =
) = 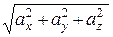 ,
,
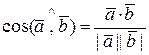 =
= 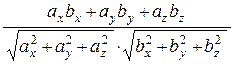 .
.
Учитывая эти формулы и следствие из свойства 6, находим:
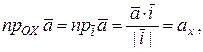
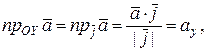
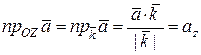 ,
,
т.е. в ДПСК координаты вектора равны его проекциям на соответствующие оси координат.
Для направляющих косинусов вектора ` а имеем
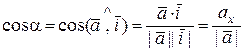 ,
,
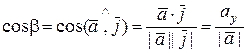 ,
,
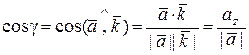 .
.
Рассмотрим орт `а о вектора ` а. Учитывая координаты вектора ` а,находим
`а о = 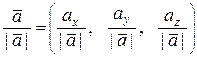 .
.
Следовательно, направляющие косинусы вектора равны координатам его орта и наоборот, т.е. можно записать `а о = (cosa, cosb, cosg).
Date: 2015-04-23; view: 531; Нарушение авторских прав