Определение 3.4

Система векторов { ₁, ₂, …, _k } ЛП L называется линейно зависимой, если существуют числа a₁, a₂, …, a _k, не все одновременно равные нулю, такие, что a_{1 1}+a_{2 2} + …+ a _{k k} =`0.

Если a_{1 1}+a_{2 2} + …+ a _{k k} =`0 тогда и только тогда, когда все коэффициенты этой линейной комбинации равны 0, то система векторов { ₁, ₂, …, _k } ЛП L называется линейно независимой.

Линейно независимая система { ₁, ₂, …, _k } называется максимально линейно независимой, если "` b Î L система { <sub>1</sub>, <sub>2</sub>, …, <sub>k</sub>,` b } – линейно зависима.

Если система { ₁, ₂, …, _k } максимально линейно независима, то равенство

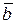a_{1 1}+ a_{2 2} + …+ a _{k k} + a _{k+ 1} =`0

выполняется, когда не все коэффициенты a _i = 0, причем обязательно a _{k+ 1}¹0. Тогда разделив обе части этого равенства на a _{k- 1}, можно записать его в форме

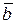= b_{1 1}+ b_{2 2} + …+ b _{k k},

т.е. представить вектор 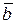в виде линейной комбинации векторов ₁, ₂, …, _k. При этом говорят, что вектор 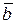разложен по векторам ₁, ₂, …, _k.

Можно доказать, что система векторов { ₁, ₂, …, _т } линейно зависима тогда и только тогда, когда хотя бы один из векторов этой системы можно представить в виде линейной комбинации остальных векторов.

Date: 2015-04-23; view: 434; Нарушение авторских прав