Энтропия. Законы механики обратимы во времени

Законы механики обратимы во времени. Любой процесс, обусловленный одним только механическим взаимодействием тел, можно провести и в прямом и в обратном направлении. Например, уроним камень с высоты h. В момент падения на Землю скорость камня будет равна 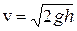. Тот же процесс в обратном направлении: бросим камень вертикально вверх с начальной скоростью 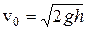. Камень поднимется на высоту h, причем его скорость в верней точки траектории будет равна нулю, а значит камень вернется в исходное состояние.

Иначе обстоит дело с процессами, происходящими в макросистемах. По сути все такие процессы являются необратимыми, т.е. могут протекать только в одном направлении. Обратимые равновесные квазистатичные процессы – это только модель, идеализация реальных процессов, удобная для рассмотрения ряда явлений. Возникает вопрос: почему реальные термодинамические процессы необратимы? Чем объясняется второй закон термодинамики? Для того, чтобы ответить на эти вопросы, Клаузиус ввел новую термодинамическую величину – энтропию.

Энтропия S – функция состояния системы, малое приращение которой dS равно отношению полученного телом малого количества теплоты dQ к температуре системы Т:

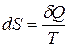. (4.1)

Единицей измерения энтропии в СИ служит джоуль, деленный на кельвин (Дж/К). Поскольку энтропия является функцией состояния, ее изменение D S при переходе из состояния 1 в состояние 2 не зависит от процесса, посредством которого осуществляется переход:

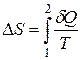. (4.2)

Энтропия – аддитивная величина, т.е. энтропия любой макросистемы равна сумме энтропий всех ее частей.

Одно из важнейших свойств энтропии заключается в том, что энтропия замкнутых (теплоизолированных) макросистем не уменьшается: в равновесных процессах энтропия остается неизменной, а в неравновесных – возрастает. Это утверждение, называемое принципом возрастания энтропии, является еще одной из эквивалентных формулировок второго начала термодинамики.

В 1906 г. немецкий физик В. Нернст[19] сформулировал теорему, согласно которой при приближении температуры системы к абсолютному нулю, ее энтропия также стремится к нулю: .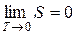

Из теоремы Нернста следует, что вблизи абсолютного нуля температуры к нулю будет стремиться также и теплоемкость С любой системы: 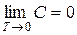. Другое важное следствие: при помощи конечной последовательности термодинамических процессов нельзя достичь температуры, равной абсолютному нулю.

Теорему Нернста невозможно строго вывести из первых двух законов термодинамики, поэтому ее часто называют третьим законом термодинамики.

Из определения энтропии (4.1) следует, что 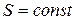при 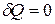. Таким образом, адиабатный процесс является изоэнтропийным, а кривая, показывающая адиабатный процесс, может быть названа изоэнтропой (см. рис. 3.4).

Выведем формулу для расчета энтропии идеального газа. Объединив определение энтропии (4.1) с первым законом термодинамики в форме (3.10), получим:

.

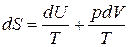Согласно (3.19) приращение внутренней энергии газа можно записать как 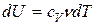. Давление газа выразим из уравнения Менделеева-Клапейрона: 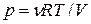. Имеем:

.

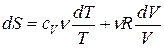Проинтегрировав это равенство, получим выражение для изменения энтропии идеального газа при переходе из состояния 1 в состояние 2:

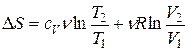. (4.3)

Задача 4.1. Найти изменение D S энтропии при изобарном расширении азота массой m = 4 г от объема V ₁ = 5 л до объема V ₂ = 9 л.

Date: 2015-05-08; view: 924; Нарушение авторских прав