Статистический смысл второго закона термодинамики

В 1872 г. Больцман установил связь между энтропией макросистемы и статистическим весом ее макросостояния. Рассмотрим этот вопрос подробно.

Ранее уже упоминалось, что состояние макроскопической системы можно описать, задав ее макроскопические параметры: объем, давление, температуру и др. Заданное таким образом состояние системы называется макросостоянием. С другой стороны, состояние системы можно охарактеризовать детально, задав состояние каждой из образующих систему молекул. Такое состояние называется микросостоянием.

Любое макросостояние может быть реализовано посредством некоторого числа различных микросостояний. Число различных микросостояний системы, соответствующих данному макросостоянию, называется статистическим весом W этого макросостояния.

В качестве примера определения статистического веса макросостояний рассмотрим систему, состоящую из четырех молекул газа, находящихся в закрытом сосуде. Найдем все возможные случаи распределения молекул между двумя половинами сосуда. Пронумеруем молекулы: 1, 2, 3, 4. Половины сосуда обозначим А и В (см. рис. 4.1).

Каждая молекула может с равной вероятностью находиться как в половине А, так и в половине В. Следовательно, вероятность того, что любая из молекул окажется в половине А, равна 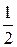. Если в половине А

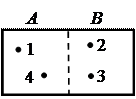
Рис. 4.1

одновременно находятся две конкретные молекулы (например, 1 и 4), то это независимые друг от друга события, следовательно, вероятность такой ситуации равна 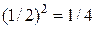. Вероятность нахождения в одной половине сосуда трех конкретных молекул равна 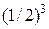, всех четырех – 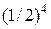. Поскольку все микросостояния системы равновероятны, то вероятность любого микросостояния равна .

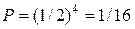В рассматриваемой нами системе возможны 5 различных макросостояний: 0 молекул в половине А, 4 – в половине В; 1 в А, 3 в В; 2 в А и 2 в В; 3 в А, 1 в В; 4 в А, 0 в В. Число микросостояний, посредством которых они реализуются, различно. Следовательно, различаются также статистический вес и вероятность реализации этих макросостояний (см. таблицу 4.1).

Таблица 4.1

Макросостояния	Способы реализации макросостояний	Стат. вес W	Вероятность Р
А	В	А	В
-		-	1,2,3,4		1/16
			2,3,4		4/16
	1,3,4
	1,2,4
	1,2,3
		1,2	3,4		6/16
1,3	2,4
1,4	2,3
2,3	1,4
2,4	1,3
3,4	1,2
		2,3,4			4/16
1,3,4
1,2,4
1,2,3
	-	1,2,3,4	-		1/16

Из таблицы видно, что самый большой статистический вес W = 6 и самую большую вероятность 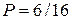имеет третье макросостояние, которому соответствует равномерное распределение молекул между половинами сосуда – 2 в А и 2 в В. В то же время макросостояние, при котором все четыре молекулы оказываются в одной половине сосуда (например, в В), реализуется только одним микросостоянием, его статистический вес и вероятность минимальны: W = 1 и .

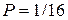С увеличением числа молекул в системе вероятность того, что все они соберутся в одной половине сосуда резко уменьшается. Например, при 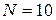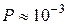, а при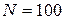 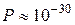. Очевидно, что при столь малой вероятности данное событие теоретически возможно, но практически не осуществимо. Вместе с тем статистический вес и вероятность макросостояния, при котором молекулы равномерно распределены по половинам сосуда быстро возрастает с увеличением N. Таким образом, предоставленная самой себе макросистема стремится перейти к наиболее вероятному состоянию.

По Больцману энтропия S больше у тех макросостояний, которые обладают большим статистическим весом:

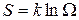. (4.4)

Иными словами, энтропия является мерой беспорядка в макросистеме, поскольку макросостояния с большей упорядоченностью (например, когда все молекулы собраны в одной половине сосуда) имеют меньший статистический вес, чем состояния с меньшей степенью упорядоченности (когда молекулы распределены равномерно или почти равномерно между половинами сосуда). Все реальные термодинамические процессы являются необратимыми, поскольку все они протекают так, что беспорядок (хаос) в макросистеме увеличивается. Любой самопроизвольный процесс заканчивается наиболее вероятным, а значит и наиболее хаотическим, разупорядоченным макросостоянием системы, которому согласно формуле (4.4) соответствует максимальное значение энтропии.

Итак, второй закон термодинамики по сути своей является статистическим законом: все процессы протекают так, чтобы система переходила от менее вероятных состояний к более вероятным. Поэтому в неравновесных процессах энтропия замкнутой системы возрастает, а в равновесных – не изменяется (т.к. все равновесные состояния системы имеют одинаковый максимально возможный статистический вес).

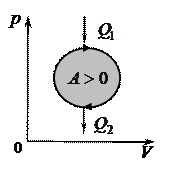
Рис. 4.2 Рис. 4.3

Date: 2015-05-08; view: 1008; Нарушение авторских прав