Решение. Мысленно разобьем сосуд на цилиндры малой высоты dh (см

Мысленно разобьем сосуд на цилиндры малой высоты dh (см. рис. 2.8). В пределах каждого такого цилиндра давление газа можно считать одинаковым. Найдем массу газа dm в цилиндре, находящемся на высоте h, для чего воспользуемся уравнением Менделеева-Клапейрона (1.9) и барометрической формулой (2.17). Имеем:

.

Общую массу газа в сосуде найдем, проинтегрировав полученное выражение по h в пределах от 0 до Н:

.

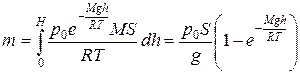Воспользовавшись основным уравнением МКТ идеального газа 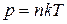из формулы (2.17) можно получить зависимость концентрации молекул газа от высоты и потенциальной энергии молекулы E_P. Обозначим n ₀ концентрацию на нулевой высоте. Имеем:

,

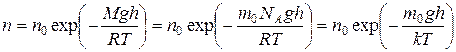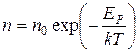. (2.18)

Формула (2.18) называется распределением молекул газа по потенциальным энергиям или распределением Больцмана.

Справедливость распределения Больцмана была в 1909 году подтверждена экспериментально французским физиком Ж. Перреном[17], который исследовал под микроскопом распределение мельчайших частиц эмульсии смолы гуммигута в воде. Результаты эксперимента совпали с расчетами, выполненными с использованием формулы (2.18).

В заключение отметим, что распределения Максвелла и Больцмана можно объединить в одно общее распределение Максвелла-Больцмана, согласно которому число молекул dN, проекции скорости и координаты которых лежат в интервале 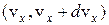, , 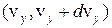, , 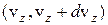, , 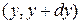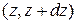можно найти как

, (2.19)

где 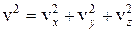, 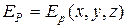- потенциальная энергия молекулы в точке с координатами .

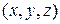Date: 2015-05-08; view: 909; Нарушение авторских прав