Работа газа

Изменить состояние (а значит и внутреннюю энергию) какого-либо макроскопического тела можно, совершив над ним механическую работу, либо позволив телу самому совершить работу против внешних сил. Найдем работу, которую совершает газ при изменении своего состояния. Поместим газ в горизонтальный цилиндр, левое основание которого площадью S жестко закреплено, а правое представляет собой подвижный поршень (см. рис. 3.2).

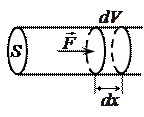
Рис. 3.2

В некоторый момент времени газ в цилиндре находится в равновесии под давлением p. Газ давит на поршень с силой . Пусть под действием этой силы поршень сместится вправо на расстояние dx, настолько малое, чтобы изменением давления газа в процессе перемещения поршня можно было пренебречь. Элементарная работа, совершенная при этом газом, равна

,

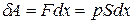, (3.4)

где 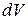- приращение объема газа. Следовательно, работу, совершенную при конечном изменении объема газа от 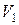до 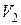, можно найти как

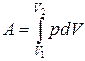. (3.5)

Из формулы (3.5) следует, что при расширении газ совершает положительную работу, а при сжатии – отрицательную; работа газа в изохорном процессе равна нулю.

Как известно, определенный интеграл, взятый от какой-либо функции на некотором интервале, численно равен площади под графиком этой функции на данном интервале. Следовательно, работу газа в произвольном равновесном процессе можно найти графически, как показано на рисунке 3.3. Обратите внимание, что работа газа в круговом процессе (т.е. в процессе, у которого начальное и конечное состояния газа совпадают), показанном на рисунке 3.3 в, равна площади замкнутой фигуры. Причем 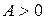, если диаграмма процесса проходится по часовой стрелке (как на рисунке), и 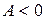, если обход производится против часовой стрелки.

а б в

Рис. 3.3

Получим выражения для работы идеального газа в изопроцессах.

Date: 2015-05-08; view: 933; Нарушение авторских прав