Элементарные сведения из теории вероятностей

Статистической физикой называют раздел физики, в котором изучаются свойства макроскопических систем, исходя из индивидуальных свойств, составляющих систему микрочастиц (например, молекул).

Любое макроскопическое тело состоит из очень большого числа молекул (10¹⁵ и больше), поэтому описать движение каждой молекулы невозможно, да и не имеет смысла. Вместо рассмотрения движения каждой микрочастицы в отдельности статистическая физика оперирует средними значениями параметров частиц и устанавливает закономерности, связывающие усредненные характеристики микрочастиц со свойствами макросистемы в целом.

В основе статистической физики лежит теория вероятностей. Вероятность какого-либо события характеризуется кратностью его повторения. Если в N случаях i -событие происходит N_i раз, то вероятностью W _i этого события называется величина

.

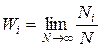Например, вероятность того, что подброшенная монета упадет «орлом» равна ½, «решеткой» - также ½. В молекулярной физике N – конечное, но, как правило, очень большое число, поэтому можно считать, что

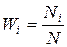. (2.1)

Вероятность того, что подброшенная монета упадет или «орлом» или «решеткой» составляет ½ + ½ = 1. Таким образом, сумма вероятностей всех возможных событий равна единице:

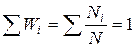. (2.2)

Рассмотрим две основные теоремы теории вероятностей.

Теорема о сложении вероятностей: вероятность того, что произойдет одно из нескольких независимых друг от друга событий, равна сумме вероятностей этих событий. Например, если Вы бросаете игральный кубик, вероятность того, что в результате N бросаний выпадет число i или число k, равна

W_{i или k} = W_i + W_k. (2.3)

Теорема об умножении вероятностей: вероятность того, что произойдут несколько независимых друг от друга событий, равна произведению вероятностей этих событий. Например, вероятность того, что при N бросаниях двух кубиков на первом выпадет i и на втором выпадет k, равна

W_{i и k} = (N_i/N)×(N_k/N) = W_i × W_k. (2.4)

Задача 2.1. Определить вероятность W того, что при броске двух кубиков в сумме наберется 3 очка.

Date: 2015-05-08; view: 1009; Нарушение авторских прав