Решение. Обозначим давление, объем и температуру газа в начальном состоянии p1, V1, T1, в конечном – p2, V2, T2

Обозначим давление, объем и температуру газа в начальном состоянии p ₁, V ₁, T ₁, в конечном – p ₂, V ₂, T ₂. По условию задачи 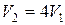. Поскольку 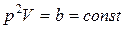, то 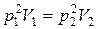, отсюда 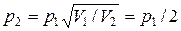. Согласно уравнению Клапейрона (1.10)

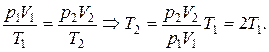
Итак, температура увеличилась в два раза.

Исторически уравнения Клапейрона (1.10) и Клапейрона-Менделеева (1.9) были получены в результате обобщения ряда газовых законов, открытых экспериментально на протяжении XVII – первой половины XIX веков. Прежде всего, это знакомые Вам по школьному курсу физики законы, описывающие изопроцессы (т.е. процессы, протекающие при неизменном количестве вещества и постоянном давлении, объеме или температуре).

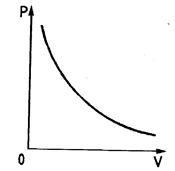
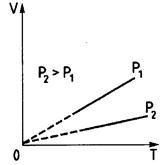
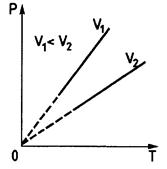
Рис. 1.4 Рис. 1.5 Рис. 1.6

Изотермический процесс. Процесс изменения состояния макроскопической системой называется изотермическим, если он протекает при постоянной температуре. Закон, описывающий изотермический процесс в идеальном газе носит название закона Бойля [10] -Мариотта [11]: для газа неизменной массы при неизменной температуре произведение давления на объем является постоянной величиной:

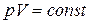при 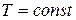. (1.11)

Из уравнения (1.11) видно, что при постоянной температуре давление газа обратно пропорционально его объему. Поэтому изотерма (т.е. зависимост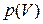и при 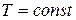) в координатах (p,V) будет изображаться гиперболой (рис. 1.4).

Изобарный процесс. Процесс изменения состояния макроскопической системы называется изобарным (или изобарическим), если он происходит при постоянном давлении. Закон, описывающий изобарный процесс в идеальном газе носит имя Гей-Люссака [12]: при неизменной массе газа и постоянном давлении отношение объема к температуре есть величина постоянная:

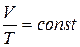при 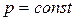. (1.12)

Из уравнения (1.12) следует, что при постоянном давлении объем газа прямо пропорционален его температуре: 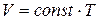. Графически эта зависимость изображается прямой, называемой изобарой (рис. 1.5).

Изохорный процесс. Изохорным (или изохорическим) называется процесс изменения состояния макросистемы, протекающий при постоянном объеме. Закон, описывающий изменение состояния идеального газа в изохорном процессе был открыт французским физиком Ж.Шарлем[13] и носит его имя. З акон Шарля: при неизменной массе газа и постоянном объеме отношение давления к температуре есть величина постоянная:

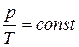при 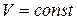. (1.13)

Из уравнения (1.13) следует, что при неизменном объеме давление газа прямо пропорционально его температуре: 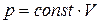. Соответствующая зависимость графически изображается прямой, называемой изохорой (рис. 1.6).

Сформулируем еще три закона, описывающие свойства идеальных газов.

Закон Авогадро: в равных объемах любых газов при одинаковых условиях содержится одно и то же число молекул.

Закон Дальтона [14]: давление смеси идеальных газов равно сумме парциальных давлений газов, входящих в ее состав. (Парциальным называется давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре).

Закон Лошмидта [15]: в 1 см³ любого идеального газа при нормальных условиях содержится одинаковое число молекул (число Лошмидта), равное см^-3.

Легко убедиться, что все приведенные выше экспериментальные газовые законы можно вывести из уравнения Клапейрона-Менделеева (1.9). Проделайте это самостоятельно в качестве упражнения.

Date: 2015-05-08; view: 1201; Нарушение авторских прав