Решение. Три очка в сумме на двух кубиках может получиться в результате двух комбинаций: «1» на первом, «2» на втором и «2» на первом

Три очка в сумме на двух кубиках может получиться в результате двух комбинаций: «1» на первом, «2» на втором и «2» на первом, «1» на втором. Обозначим вероятность этих комбинаций W _{1 и 2} и W _{2 и 1}. Согласно теореме о сложении вероятностей (2.3) искомая вероятность W = = W _{1 и 2} + W _{2 и 1} = 2 W _{1 и 2}. Вероятность выпадения какого-либо числа на кубике равна 1/6 (поскольку всего возможных событий 6, все они равновероятны, и их сумма, согласно (2.2), равна единице). По теореме об умножении вероятностей (2.4) находим W _{1 и 2} = 1/36. Вероятность того, что на двух кубиках в сумме выпадет три очка, равна W = 2/36 (»5,6 %).

Среднее значение 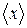дискретной величины x можно найти, зная вероятности появления ее значений:

.

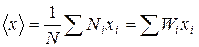Рассмотрим случай, когда величина x является непрерывной (например, скорость молекул) и может случайным образом принимать значения из некоторой области (х ₁, x ₂). Разобьем всю область изменения величины x на малые интервалы D х. Пусть нам известна вероятность D W_x попадания величины х на интервал D х. Зависимость

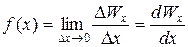(2.5)

называется функцией распределения величины х. Функция f (x) имеет смысл плотности вероятности, т.е. численно равна вероятности того, что рассматриваемая величина окажется в единичном интервале вблизи значения x.

Один из возможных видов функции распределения изображен на рисунке 2.1. Из определения (2.5) следует, что вероятность обнаружения случайной величины в пределах интервала равна площади заштрихованной полоски шириной dx, показанной на рисунке.

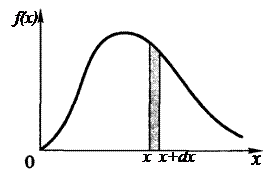
Рис. 2.1

Вероятность попадания величины x в конечный интервал (a,b) равна

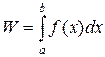. (2.6)

Вероятность того, что случайная величина x примет какое-либо значения из своей области изменения, равна 1. Следовательно, интеграл от функции распределения, взятый по всей области (х ₁, x ₂), равен единице:

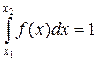. (2.7)

Выражение (2.7) называется условием нормировки функции распределения, а интеграл, стоящий в его левой части – нормировочным интегралом. Из условия нормировки следует, что площадь под графиком f (x) всегда равна единице.

Зная функцию распределения f (x), можно найти средние значения x и произвольной функции g (x):

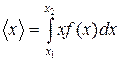и 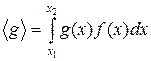. (2.8)

Date: 2015-05-08; view: 728; Нарушение авторских прав