Полосы равной толщины

Если пластинка имеет различную толщину (например, клиновидная), при падении на неё параллельного пучка лучей разность хода будет зависеть от толщины.

Для наблюдения интерференционной картины необходимо сфокусировать прибор на поверхность пластинки. Для всех участков пластинки, у которых толщина имеет одно и то же значение, условие образования максимумов и минимумов будет одинаковое. Поэтому линии максимумов и минимумов в интерференционной картине будут проходить по точкам, соответствующим равным толщинам пластинки. Такие интерференционные полосы называются полосами равной толщины. Они локализованы на поверхности пластинки.

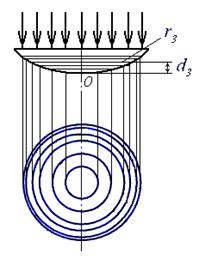
Частный случай полос равной толщины – кольца Ньютона. Для их получения плосковыпуклую линзу большого радиуса кривизны выпуклой стороной кладут на плоскопараллельную пластинку. Полосы равной толщины возникают в результате интерференции волн, отраженных от границ прослойки между сферической поверхностью линзы и поверхностью плоской пластинки (рисунок 4,б). Интерференционные полосы, возникающие в такой системе, имеют вид концентрических окружностей – колец Ньютона (рисунок 4,а).

Рассчитаем радиусы колец Ньютона. При нормальном падении лучей и большом радиусе кривизны поверхности линзы можно пренебречь различными углами падения на сферическую поверхность.

а

б

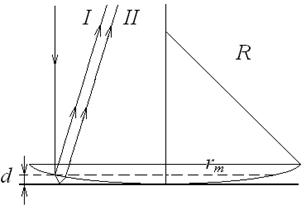
Рисунок 4 – Кольца Ньютона: а) образование колец Ньютона на экране; б) схема получения и расчета радиусов колец Ньютона

Оптическая разность хода δ определяется толщиной воздушного зазора d и равна δ =2 dn, где n – показатель преломления воздушного зазора (n =1). Из рисунка 4,б видно, что

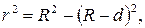
(15)

где r – радиус кольца Ньютона; R – радиус кривизны линзы; d – толщина воздушного зазора. Возведя в квадрат обе части уравнения, получим r ² = R ² – R ² + 2 Rd – d ². Ввиду малости d можно пренебречь величиной d ²

и уравнение примет вид r ² = R ² – R ² + 2 Rd. Отсюда выразим d = r ²/2 R. Если воздушный зазор заменить жидкостью с показателем преломления n ₁, оптическая разность хода будет равна δ = 2 dn ₁ = r ² n ₁/ R. Так как толщина воздушного зазора d ~ r ², то зазорам разной величины соответствуют кольца Ньютона с разными радиусами, величина которых изменяется по закону 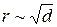, т.е. чем дальше кольца Ньютона от центра, тем они более узкие.

Необходимо учесть, что при отражении от границы раздела стекло-воздух, фаза луча I не изменится (луч отражается от оптически менее плотной среды), при отражении от границы воздух-стекло фаза луча II изменится на π (луч отражается от оптически более плотной среды). Поэтому условия минимума, т.е. условие образования темных колец в отраженном свете для воздушной прослойки

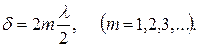
(16)

Следовательно, 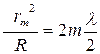или радиус m -го кольца Ньютона равен

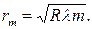
(17)

Измеряя радиусы темных колец Ньютона и зная длину волны падающего света, можно рассчитать радиус кривизны сферической поверхности линзы. Однако эта формула не может быть применена для опытной проверки, поскольку на поверхности даже хорошо очищенного стекла всегда присутствуют пылинки. Поэтому стеклянная линза не примыкает плотно к плоскопараллельной пластинке, между ними всегда имеется незначительный зазор, и возникает дополнительная разность хода, которую невозможно измерить непосредственно. Её можно исключить, измерив радиусы двух различных колец r_k и r_m. Преобразуя формулу (17) для разности квадратов радиусов двух различных колец Ньютона, получим

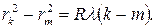
(18)

Отсюда получим выражение для радиуса R кривизны линзы

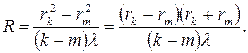
(19)

В области соприкосновения линзы с пластинкой δ = λ /2 (оптическая разность хода равна λ /2), т.е. выполняется условие минимума в отраженном свете. Поэтому в центре интерференционной картины в отраженном свете будет темное пятно радиусом r ₀. В проходящем свете центральное пятно будет светлым.

Отклонение линзы от правильной сферической формы (наличие микронеровностей) проявляется в искривлениях интерференционных колец (рисунок 5).

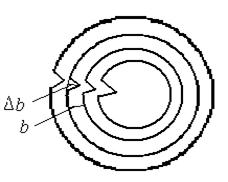
Рисунок 5 – Искривление колец Ньютона

Глубина микронеровностей приближенно определяется по формуле

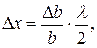
(20)

где Δ b – глубина искривления; b –ширина той же интерференционной полосы. Формула для определения глубины микронеровностей является приближенной и может быть использована только для малых Δ x, при которых Δ b < b.

Date: 2015-05-08; view: 1633; Нарушение авторских прав