Условие максимума и минимума при интерференции волн

Мгновенные значения складываемых колебаний, возбуждаемых волнами, равны

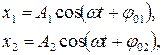
(2)

где φ ₀₁ и φ ₀₂ – начальные фазы колебаний.

Для световой волны под x понимают напряженность электрического поля 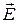или напряженность магнитного поля .

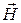Амплитуда результирующего колебания в данной точке

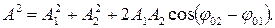
(3)

Так как волны когерентны, то cos (φ ₀₂ – φ ₀₁) имеет постоянное значение во времени (но свое для каждой точки пространства), поэтому, учитывая, что интенсивность света I пропорциональна квадрату амплитуды колебаний (I ~ A ²), интенсивность результирующего колебания равна

(4)

В точках пространства, где cos (φ ₀₂ – φ ₀₁) > 0, интенсивность I > I ₁+ I ₂; в точках, где cos (φ ₀₂ – φ ₀₁) < 0, интенсивность I < I ₁+ I ₂.

Следовательно, при наложении двух (или нескольких) когерентных волн происходит пространственное перераспределение интенсивности, в результате чего в одних местах возникают максимумы, а в других минимумы интенсивности, что и представляет собой интерференционную картину.

Для некогерентных волн разность фаз (φ ₀₂ – φ ₀₁) непрерывно меняется, поэтому среднее значение cos (φ ₀₂ – φ ₀₁) равно 0, а интенсивность всюду одинакова и при I ₁= I ₂ равна 2 I ₁.

Допустим, две когерентные волны ξ ₁ и ξ ₂, испускаемые источниками S₁ и S₂, интерферируют в точке В (рисунок 2). Здесь x ₁ и x ₂ – расстояния, пройденные волнами от источников до точки их интерференции; Δ x – геометрическая разность хода – разность расстояний пройденных 1-ой и 2-ой волнами до точки В.

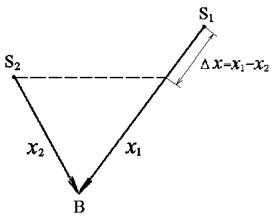
Рисунок 2 – Геометрическая разность хода Δ x = x ₁– x ₂

Запишем

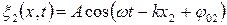– уравнение 1-ой волны; – уравнение 2-ой волны.

(5)

Разность фаз складываемых волн равна

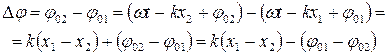
(6)

Если φ ₀₂= φ ₀₁, то ∆ φ = k ·(x ₁– x ₂)= k ·∆ x, где k =2 π / λ – волновое число. Максимальное значение cos Δ φ имеет при Δ φ =2 mπ и минимальное при Δ φ =(2 m +1) π, где m = 0,1,2,…

Условия максимума и минимума при интерференции выглядят так:

(7)

Условие φ ₀₁= φ ₀₂ необязательно, т.к. если оно не будет соблюдено, то максимумы (минимумы) результирующих колебаний только сместятся в другие точки волнового поля.

Если Δ φ =const, то и ∆ x =const.

Условия максимума и минимума при интерференции можно записать для геометрической разности хода ∆ x, учитывая, что k =2 π / λ:

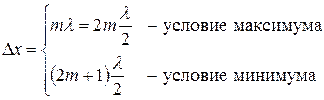
(8)

Если в разности хода укладывается четное число полуволн, то в точке интерференции наблюдается максимум. Если в разности хода укладывается нечетное число полуволн, то наблюдается минимум.

Интерференция от обычного источника света наблюдается при условии, если разность хода ∆ x интерферирующих лучей много меньше средней длины когерентности ∆ L

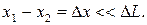
(9)

Если ограничить размеры светящейся поверхности обычного источника света, а испускаемый ею узкий пучок лучей разделить на два, которые после прохождения разных оптических путей накладываются друг на друга, то возникает интерференционная картина как от двух когерентных источников. При этом необходимо, чтобы перекрывались большие части цуга синусоиды. Этот метод используют для получения световых когерентных волн.

Ограниченность длины цуга ∆ L показывает, что волна не является строго монохроматической и ей соответствует некоторый спектральный интервал длин волн λ + ∆ λ, где λ – средняя (преимущественная) длина волны, а ∆ λ – ширина спектрального интервала.

При сложении световых волн, распространяющихся в неоднородной среде (воздух–стекло), рассматривается не геометрическая разность хода, а оптическая, т.к. необходимо учитывать показатели преломления сред, в которых распространяются световые волны.

Произведение геометрического пути на показатель преломления n среды называется оптическим путем. Величина δ = x ₁ n ₁– x ₂ n ₂ называется оптической разностью хода.

Для световых волн, распространяющихся в разных средах, условия максимума и минимума интерференции выглядят так:

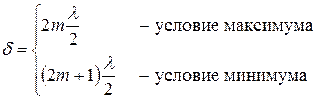
(10)

Различают два вида интерференционных полос – полосы равного наклона и полосы равной толщины.

Date: 2015-05-08; view: 6300; Нарушение авторских прав